Содержание: Термодинамика
Эта заметка открывает цикл, связанный с классической термодинамикой. Также в ней на примере температуры будет рассмотрена позиция ван Фраассена: два вопроса ниже, относящиеся к любой физической величине, неразрывно связаны между собой и образуют герменевтический круг. На примере температуры:
- Что такое температура?
- Что считается измерением температуры?
Речь, конечно, не идет про то, что температура не существует, пока ее не измеряют. Речь идет про то, что такое температура. С моей точки зрения такое рассмотрение в особенности подходит к классической термодинамике; этот путь в дальнейшем поможет лучше понять, что такое энтропия.
Начнем с небольшого исторического обзора. Кожа человека содержит терморецепторы, что позволяет ему распознать холод и тепло и этого было достаточно для большей части истории человечества. После появления технологий, связанных с высокими температурами (изготовление качественной стали или стекла), необходимый температурный режим выбирался посредством зрения. Это умение на протяжении веков передавалось от мастера к подмастерью.
Интересно отметить, что температура и темперамент имеют общее происхождение от латинского слова смешивать. В теории темперамента Галена в основы поведения людей были заложены категории горячий-холодный и сухой-влажный, а правильный темперамент достигался надлежащей смесью этих начал.
Филон Византийский (3 век до н. э.) сконструировал специальный прибор для доказательства, что объем воздуха зависит от температуры; от стеклянного шара с воздухом отходила трубка, заканчивающаяся в соседнем сосуде с водой. Изменение температуры воздуха в шаре приводило либо к выводу воздуха через трубку в случае повышения температуры, либо к втягивания воды при понижении температуры. Герон Александрийский (1 век н.э) широко использовал этот принцип в конструкциях многих устройств; расширение воздуха при нагревании использовалось для создания движения. Перевод книги Герона Пневматика в 16 веке на итальянский и латынь дали толчок к созданию первого термометра, который по конструкции был похож на устройство Филона.
Точно нельзя сказать, кому принадлежит приоритет создания первого термометра, поскольку идея витала в воздухе. Многие соглашаются с притязаниями Галилея, который в 1597 году описал эксперименты с прибором, аналогичным таковому у Филона — см. рисунок из Вики ниже:
Изменение температуры ведет к изменению высоты столбика воды. Правда, следует отметить, что эксперименты Галилея носили качественный характер без введения температурной шкалы. Отто фон Герике, Санторио, Дреббель и др. внесли вклад в усовершенствование газового термометра, но затем работа в этом направлении остановилась. Пришло осознание, что газовый термометр одновременно является барометром; другими словами его показания зависят в том числе от давления. Отмечу, что в то время эксперименты с давлением воздуха только начинались и барометр как таковой еще не существовал.
В качестве рабочего тела стали использовать жидкость: спирт или ртуть. Один из первых термометров был изготовлен во Флорентийской академии (1641 г.), далее следует отметить работы Даленсе, Галлея, Гюйгенса, Гука, Ренальдини и др. Наибольшего успеха в технологии изготовлении надежных термометров достигли Фаренгейт и Реомюр (1740 г.). Для калибровки термометров применялись разные реперные точки и также использовались разные шкалы. В конце концов остановились на температурах плавления льда и кипения воды со стоградусной шкалой (Цельсий, 1742 г.).
В то же время обнаружилась проблема с жидкостными термометрами — расширение жидкости происходило неравномерно. Делюк (1772 г.) сравнил спиртовой и ртутный термометры между собой и показал, что в середине интервала они показывают разные температуры. Расширение ртути было более равномерным и в качестве стандартного стали использовать ртутные термометры. Тем не менее, привязка температурной шкалы к определенному телу была проблематичной. Вопрос можно поставить таким образом: зависит ли коэффициент расширения ртути от температуры или нет.
Возвращение к газовому термометру началось еще в период разработки жидкостных термометров в 1702 году в работах Гийома Амонтона. Принцип работы газового термометра показан на рисунке из Вики ниже:
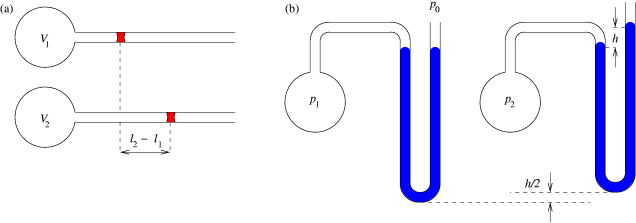
Слева показан принцип газового термометра постоянного давления, он по сути дела аналогичен прибору Галилея. Амонтон разработал газовый термометр постоянного объема — схема справа. Отличие заключается в том, что при изменении температуры подбирают количество жидкости для поддержания объема газа постоянным. Это в свою очередь позволяет измерять температуру по разнице высоты столбиков жидкости.
Амонтон далее изучал зависимость расширения воздуха от температуры. На основании измерений он предсказал существование абсолютного нуля на шкале температур, когда объем газа должен был бы достичь нуля. Но газовому термометру для достижения статуса надежного измерительного инструмента потребовалось длительное время. Были открыты и исследованы различные газы; было установлено, что поведение всех газов при низких давлениях описывается уравнением состояния идеального газа. Это предполагало, что в этом случае измерение температуры не зависит от рабочего тела. На этом пути также вернулась идею абсолютного нуля температур, выдвинутая Амонтоном. Отмечу, что поведение реальных газов несколько отличается от уравнения идеального газа и необходимо введение поправок.
В конечном итоге именно газовый термометр стал рассматриваться как наиболее точное устройство для измерения температуры и он стал использоваться для калибровки других термометров. В 1889 г. была принята первая международная практическая температурная шкала на основе водородного газового термометра постоянного объема с двумя реперными точками. Большую роль в принятии этого стандарта сыграли экспериментальные работы физика Пьера Шаппюи (Pierre Chappuis). В девятнадцатом веке появились другие методы измерения температуры — термопара, термосопротивление и пирометры, но для рассмотрения ниже остановимся на жидкостных и газовых термометрах.
Вначале рассмотрим общий вопрос. Он связан с тем, что нередко можно услышать о неизмеряемости энтропии. В этой связи полезно обсудить измеряемые величины на примере температуры, давления и объема (длины). Жидкостные и газовые термометры показывают температуру непосредственно. С другой стороны, реально измеряется высота ртутного или спиртового столбика. Длина пересчитывается в температуру посредством шкалы, которая откалибрована на предположении об уравнении состояния рабочего тела.
Следует ли сказать, что непосредственно измеряемой величиной является длина (объем), а температура на самом деле является косвенно измеряемой величиной? Ситуация однако сложнее, поскольку нельзя забывать про тепловое расширение твердых тел; оно мало, но не равно нулю. Например, при разработке стандарта метра в 1875 году было необходимо определить тепловое расширение выбранных стандартов длины на основе сплавов платины с иридием. Каждому национальному прототипу метра прилагались два ртутных проградуированных термометра для внесения соответствующих поправок на изменение температуры.
Таким образом, строго говоря измерение всех трех величин на уровне рассмотренных технологий зависит друг от друга и это нельзя забывать. Если при измерении длины горячего тела линейка нагревается, то необходимо ввести соответствующие поправки. Так устроена настоящая метрология — поправка поправку подгоняет. С другой стороны, наличие измерительных инструментов, которые показывают физическую величину, относящуюся к состоянию тела, позволяет говорить о непосредственном измерении этой величины. Возвращаясь к энтропии следует сказать, что непосредственное измерение энтропии в таком духе невозможно, что однако не мешает в конечном итоге получать численные значения энтропии тела.
Теперь вернемся в вопросам ван Фраассена. Он рассматривает их при обсуждении проблемы координации (термин Эрнста Маха) — каким образом величина из математического уравнения сопоставляется с таковой в реальном мире. В нашем случае следует сказать, что для тела существует определенное уравнение состояния:
f(p, t, V) = 0 или V(p, t) или p(t, V) или t(p, V)
где p — давление, t — практическая температура, V — объем. Каким образом мы сопоставляем буковки из этого уравнения с состоянием тела? Объем и давление оставим на интуитивном уровне, когда объем связывается с измерением линейкой и геометрией, а давление с силой. Рассмотрим этот вопрос на примере температуры. При этом вопрос не стоит в выборе той или иной шкалы, поскольку произвольность численных значений, связанных с выбором масштаба измерений исключить нельзя. Вопрос связан с тем, что мы называем температурой в реальном мире.
Два вопроса ‘Что такое температура?’ и ‘Что считается измерением температуры?’ оказываются сильно переплетены между собой. Их отделение друг от друга возможно в случае сложившей теории, которая позволяет найти в мире физический коррелят температуры и таким образом понять, что считается измерением температуры.
В классической термодинамике для этого используется нулевой закон термодинамики, который вводит в рассмотрение существование практической температуры. Наименование нулевой связано с тем, что его сформулировали после первого и второго законов термодинамики. Ученые обратили внимание, что для начального обсуждения и построения термодинамики требуется понятие температуры, но таковое в механике отсутствует.
Возьму такую формулировку. Существует функция состояния температура, которая при достижении равновесного состояния между двумя телами принимает одно и то же значение для обоих тел. Температура также является транзитивным свойством. Сказанное означает, что при контакте между термометром и телом через некоторое время температура термометра и тела становятся равными. Транзитивность означает, что если термометр показывает одно и то же значение при измерении температуры двух разных тел, то из этого следует, что температуры тел равны между собой.
Формальное утверждение выше вполне достаточно для построения практической шкалы температур. Возможное возражение может быть связано с тем, что в нем не сказано, что такое температура. В этом состоит как сила, так и слабость классической термодинамики. Преимущество заключается в том, что нам не требуется вводить дополнительные сущности, нулевого закона термодинамики вполне достаточно для построения физического коррелята температуры и тем самым размыкания герменевтического круга с двумя вопросами выше. Недостаток связан с присущим человеку желанием познать суть вещей.
Обычно в этом месте сразу же переходят к молекулярно-кинетической теории, где дается интерпретация температуры в духе средней скорости движения молекул. Я намеренно не буду переходить на этот уровень по ряду причин. Классическая термодинамика является замкнутой теорией и в этом смысле она не зависит от молекулярно-кинетической теории. Более того, знакомство с энтропией на уровне статистической термодинамике без знания классической термодинамики является по-моему основной причиной непонимания того, что такое энтропия. Точно также рассмотрение вопроса о сводимости классической термодинамике к статистической механике требует хорошего знания классической термодинамики.
В дополнение к нулевому закону термодинамики нам требуется утверждение о существовании уравнения состояния для тела с постоянной массой, то есть о связи температуры, давления и объема между собой. Для создания температурной шкалы нам требуется представление о конкретном уравнения состояния. Уравнение состояния идеального газа дает намек на существование универсальной шкалы температур с абсолютным нулем, но пока это остается на уровне предположений. Отмечу, что дальнейшее рассмотрение в классической термодинамике позволяет ввести термодинамическую шкалу температур.
Дополнительно требуется знание о постоянстве температур фазовых переходов. Строго говоря, температура плавления льда и кипения воды зависят от давления и это также необходимо учитывать при проведении измерений. Этот вопрос также решается в рамках классической термодинамики.
Сказанного выше вполне достаточно для понимания истории термометрии с точки зрения настоящего. Можно сказать, что измерялось в том или ином термометре и какие поправки требовалось бы ввести для получения современной практической температуры. Существование сложившейся теории позволяет увидеть физический коррелят температуры и дать правильную интерпретацию проводимых по ходу истории экспериментов, связанных с температурой.
Можно ли разрешить герменевтический круг по ходу истории, то есть, глядя на проводимые эксперименты глазами современников? Например, Смородинский замечает:
‘История о том, как научились измерять температуру, интересна и необычна. Термометры были придуманы за много лет до того, как люди поняли, что именно они измеряют.’
Это правильное утверждение, но несмотря на это есть все основания для положительного ответа на заданный вопрос, поскольку в конечном итоге теории были созданы по ходу исторического развития.
Я не нашел хорошего описания размышлений ученых тех времен над увиденным при использовании ртутных и газовых термометров, в особенности в 17-ом и 18-ом веке. С другой стороны, это увело бы нас слишком далеко в сторону. Самое важное заключалось в том, что не было понимания разницы между температурой и теплотой; эта разница сформировалась как раз в ходе становления термометра как инструмента измерения. Постепенно стало понятно, что термометр измеряет именно температуру, а теплота представляет собой другую физическую величину. Это вопрос будет рассмотрен отдельно.
Бас ван Фраассен отмечает, что в ходе исторического развития герменевтический круг разрывается, если в ходе проведения и обсуждения результатов экспериментов в конечном итоге удается достичь появления стабильной теории. Проводимые эксперименты приводят к первоначальной интерпретации (например, термометр измеряет теплоту), которая далее рушится при проведении и обсуждении последующих экспериментов. В то же время ученые при проведении экспериментов понимают сделанное с практической стороны дела, что в свою очередь дает возможность рационального обсуждения происходящего. В духе Бруно Латура можно сказать, что конструируемые факты (термометр измеряет теплоту) оказывались неустойчивыми и требовалась их модификация до достижения устойчивости (термометр измеряет температуру).
Важно отметить, что тепловое расширение твердых тел мало и можно было пренебречь изменением корпуса термометра при повышении температуры. Влияние давления на объем жидкости также невелико — им можно пренебречь в интервале изменения атмосферного давления. Таким образом, использование жидкостных термометров приводило к стабильным результатам. Зависимостью воздуха и газов от давления пренебречь было уже нельзя, но параллельно появились барометры, которые позволили изучить уравнение состояния газов. По мере увеличения точности измерений можно было включить в рассмотрение поправки, связанные с расширением твердых и жидких тел, в том числе с влиянием давления и неидеальности реальных газов.
Далее: Уравнение состояние идеального газа
Информация
Я. А. Смородинский. Температура, 2-е изд., 1987.
Т. Куинн, Температура, 1985.
T. J. Quinn, Temperature, 1983.
Bas C. van Fraassen, Scientific Representation: Paradoxes of Perspective, Part II: Windows, Engines, and Measurement, 2008.
См. также
Проблема координации. Температура как физическая величина: Математика, физика и измерение. Измерение температуры в настоящее время. История термометрии. Проблемы выбора рабочего вещества для термометра. Температура, теплота и термодинамическая шкала.