Previous: Chapter 2. From Caloric Theory to Thermodynamics
The main goal of this chapter is to move from the first and second laws of thermodynamics to tables of the thermodynamic properties of substances. Thermodynamics can be used to solve practical problems only if the properties of substances are available, which must be obtained through specific experiments. This also provides insight into the relationship between internal energy, entropy and experiments, thereby providing an answer to the problem of coordination. For brevity, in my discussion I use calorimetry and the thermal equation of state only, although there are other experiments whose results are also employed to derive the thermodynamic properties.
We begin with a discussion of calorimetry and then move on to the fundamental equation that combines the first and second laws. The internal energy in temperature and volume, U(T, V), is called the caloric equation of state. In addition to heat capacities, extra experiments are required to derive it. However, introduction of the entropy, S(T, V), not only does not require new experimental data, but even allows us to replace these extra experiments with information from the thermal equation of state.
The fundamental equation of thermodynamics is obtained with entropy and volume as independent variables. The Legendre transformation allows us to transform the fundamental equation into more convenient form with other independent variables, yielding new state functions — enthalpy (H), Helmholtz energy (A), and Gibbs free energy (G). These transformations do not require new experimental data, but their use facilitates the practical application of the equations of classical thermodynamics.
In conclusion, the reference book ‘NIST-JANAF Thermochemical Tables‘ is reviewed. The information from similar reference book is used in Chapter 1.5 ‘Adiabatic Flame Temperature‘; thus, this chapter already has some relevance to candle combustion.
- Calorimeter and state functions
- The fundamental equation of thermodynamics
- Legendre transform and new state functions
- Thermodynamic tables
Calorimeter and state functions
The calorimeter has been examined in the previous chapter. In this section, we relate the measurement of heat in a calorimeter to state functions. Let us rewrite the first law as follows:
dQ = dU + pdV
At constant volume, no expansion work occurs and the measured heat at constant volume (Qv) is equal to the change in internal energy:
dQ v = dU => Q v = Δ U
From measurements of heat at constant volume, the heat capacity at constant volume is determined:
Cv = (∂Q/∂T)v = (∂U/∂T)v
Experiments in calorimetry are typically conducted at constant pressure, so an equation for the amount of heat measured at constant pressure (Qp) is required. In this case, it is convenient to introduce a new thermodynamic function, enthalpy: H = U + pV . Below, we consider this equation as an example of the Legendre transformation, which allows for a change of variables in the fundamental equation of thermodynamics. In this section, we simply consider the process to measure the amount of heat at constant pressure:
dQp = dU + pdV = d(U + pV) => Qp = ΔH
Thus, measuring the amount of heat at constant pressure yields the change in the enthalpy. This equation also shows that enthalpy differs from internal energy in terms of expansion work, but it is important to remember that this only applies to processes at constant pressure.
In any case, enthalpy turns out to be a function of state, which is convenient to use when processing information from calorimetric experiments to measure heat capacity at constant pressure:
Cp = (∂Q/∂T)p = (∂H/∂T)p
In principle, it would be possible to use the results of these experiments to calculate the change in internal energy, but this would require the use of a thermal equation of state. Using enthalpy allows us to separate the processing of constant-pressure calorimetry results from the experiments investigating the thermal equation of state. Furthermore, many calculations are performed using the independent variables pressure and temperature, and in this case, it is more convenient to use enthalpy. Thus, enthalpy, not internal energy is given in the table of thermodynamic properties.
The ice calorimeter was used, among other things, to determine the heat released during chemical reactions, primarily combustion reactions. Carnot’s ideal heat engine runs with ideal heat sources, while in the real world, the energy of chemical reactions is used instead. One of the first researchers to study the heat of combustion in the first half of the 19th century was Germain Hess, who worked at the St. Petersburg Academy of Sciences. He formulated the Hess law:
‘When any chemical compound is formed, the same amount of heat is always released, regardless of whether the formation of this compound occurs directly or indirectly in several stages.’
Nowadays, we should talk about reaction enthalpies, where the enthalpy of a reaction is the difference in the enthalpies of the products and reactants, when the enthalpies of all substances are taken at the same temperature and pressure. For example, for the reaction of coal combustion:
C(coal) + O2 = CO2
∆rH = Hm(CO2, T, P) ‐ Hm(C, coal, T, P) ‐ Hm(O2, T, P)
For extensive quantities, thermodynamic functions depend on the mass. Tables typically list values for one mole of the substance, which is indicated by the subscript m (molar enthalpy).
In thermodynamics, only the change in enthalpy (internal energy) can be determined, so to obtain numerical values, molar enthalpies of formation of substances are introduced — that is, the enthalpies of the reaction of formation of one mole of a substance from simple substances in the standard state (∆fHm). These are given in the reference book and are employed to calculate reaction enthalpies.
The fundamental equation of thermodynamics
Substituting the heat from the second law of thermodynamics into the first law yields a combined equation of the first and second laws, called the fundamental equation of thermodynamics. Due to the inequality in the second law, two variants appear, the fundamental equation:
dU = TdS ‐ pdV
and the fundamental inequality:
dU < TexdS ‐ pexdV
It is important not to confuse one with the other. The inequality uses temperature and pressure, determined by external conditions. Thus, the inequality also includes the substance state with temperature and pressure gradients. The inequality defines a criterion for a spontaneous process under given external conditions and thus allows us to derive a criterion for equilibrium. In the next chapter we consider the fundamental inequality and examples to employ it to determine equilibrium.
In this chapter, we consider the fundamental equation, which assumes that we are dealing with a substance state of uniform temperature and pressure; the form of the equation emphasizes that temperature and pressure gradients are excluded from consideration. Integrals from the fundamental equation correspond to equilibrium processes, but the results obtained this way will be the same for all processes, including non-equilibrium ones.
A simple example: if we know the volume magnitude in two states, then the change in volume will be the difference between these quantities, regardless of how the process occurred. The same logic applies to all thermodynamic functions of state — internal energy, entropy, enthalpy, Helmholtz energy, and Gibbs free energy; this is the meaning of the concept of a state function. However, the fundamental equation above is limited to a pure substance without chemical and phase reactions. Treatment of solutions requires to include in the fundamental equation chemical potentials.
Heat happens not to be a function of state, and the term caloric equation began to refer to internal energy U(T, V) as a function of temperature (T) and volume (V). Formally, the differential of internal energy in these variables is written as follows:
The first derivative is the heat capacity at constant volume (related to calorimetry), but determining the second derivative requires special effort. In the history of 19th century physics, Gay-Lussac and Joule’s experiments with gases led to the conclusion that this derivative is zero for gases. However, with increased accuracy, it turned out that this conclusion is valid for the ideal gas equation of state only, while for real gases the situation is more complex (Joule-Thomson experiments). I will not go into this history for brevity; for interested, it can be found elsewhere, see ‘Caloric Equation of State: Gay-Lussac and Joule-Thomson Experiments‘ in the section Additional Information.
Now let us consider entropy as a function of state S(T, V). Formally, it gives rise to two new derivatives:
However, substituting this equation into the fundamental equation of thermodynamics dU = TdS ‐ pdV gives a connection between these derivatives and the derivatives of internal energy with respect to temperature and volume:
In classical thermodynamics, Maxwell relations express the derivative of entropy with respect to volume through the thermal equation of state (see Helmholtz energy below for the derivation):
All together leads to the expressions for the internal energy U(T, V) and entropy S(T, V) as follows:
Thus, to determine the internal energy and entropy of a pure substance, information on the heat capacity at constant volume and the thermal equation of state are sufficient. Experiments in calorimetry and the study of the thermal equation of state (relative pressure coefficient) together lead to internal energy and entropy functions.
A few words about understanding entropy. The two equations above demonstrate that the relationship between internal energy, entropy and experiments conducted is pretty similar — the same experiments allow us to derive both physical quantities. Of course, these equations cannot be considered as definitions of internal energy and entropy. The definitions are the first and second law, respectively; these equations follows from them but they provide a connection to experiments.
In this context, it is worth considering whether you can already answer the question, ‘What is heat capacity at constant volume?’. This allow you to better understand expectations for the answer to the question, ‘What is entropy?’; I will return to it in the final chapter of this part.
Legendre transform and new state functions
In the fundamental equation of thermodynamics, entropy and volume act as independent variables, and internal energy, temperature, and pressure are functions: U(S, V), T(S, V), p(S, V). Note that temperature is the derivative of internal energy with respect to entropy: T = (∂U/∂S)V; this equation is used in extended irreversible thermodynamics and in statistical mechanics to define temperature.
In the previous section, the independent variables (S, V) were transformed to (T, V) without change in the fundamental equation. However, it is more convenient to change variables directly in the fundamental equation, as this provides a convenient way to solve practical problems. Legendre transformations allow us to achieve this goal. Thus, enthalpy (H = U + pV) is a Legendre transformation that swaps pressure and volume — pressure becomes the independent variable, and volume is the derivative of enthalpy:
dH = TdS + Vdp
The Helmholtz energy (A = U − TS , old notation for Helmholtz energy is F) swaps temperature and entropy, and the Gibbs energy (G = U + pV − TS = H − TS) is a double Legendre transform that swaps both pairs of variables:
dA = −SdT − pdV
dG = −SdT + Vdp
The Maxwell relation in the previous section is derived from the expression for the Helmholtz energy; it is a result of the equality of the mixed derivatives in function A(T, V). The equations above represent formal mathematical definitions of new functions of state. These mathematical operations add nothing to the first and second laws of thermodynamics. Basically, the internal energy U(S, V), the enthalpy H(S, p), the Helmholtz energy A(T, V), and the Gibbs energy G(T, p) are equivalent, since knowledge of one of them allows us to obtain the others by means of mathematical transformations.
The Gibbs energy is widely used in practical calculations, as the use of its independent variables (temperature and pressure) corresponds to the conditions of many experiments where temperature and pressure are specified as external conditions. The Helmholtz energy, on the other hand, is actively used in equilibrium statistical mechanics; it is directly related to the partition function, which in turn is used to compute thermodynamic properties from molecular properties.
The introduction of new thermodynamic functions in classical thermodynamics ‘for convenience’, evokes a certain cognitive dissonance. This allows us to once again discuss the relationship between mathematics and the world. For example, the question arises whether enthalpy, Helmholtz energy, and Gibbs free energy exist. Using enthalpy as an example, the answer is as follows. If a substance has state functions — internal energy, pressure, and volume — then it also has a property that is expressed as enthalpy: H = U + pV. In this context, the expression ‘for convenience’ is associated with the possibility in mathematics for equivalent transformations. This, of course, raises difficult questions for metaphysicians concerned with the ‘real’ structure of the world — whether internal energy, enthalpy, Helmholtz energy, or Gibbs energy exist. But none of this poses problems when solving practical tasks.
Thermodynamic tables
The reference book ‘NIST-JANAF Thermochemical Tables’ was a product of the Cold War: JANAF = Joint Army-Navy-Air Force. The name of a Soviet reference book ‘Thermodynamic Properties of Individual Substances‘ was more peacefull but the purpose was the same. The development of both books was related to the problem to estimate jet thrust by rocket launching.
Thermodynamic tables from both books can now be found online:
NIST-JANAF Thermochemical Tables
In Russian: Thermodynamic properties of individual substances
Thermodynamic tables organize the results of a huge number of experimental measurements in a convenient format for calculating the Gibbs energy of chemical reactions and then calculating the equilibrium composition. Currently, tables in this form are obsolete, as the entire procedure is automated in software; GUI allows us to search the database for the required Gibbs energies and then compute the equilibrium composition by means of numerical algorithms.
The tables are based on the chemical identification of pure substances; each substance has its own table, in which thermodynamic properties are tabulated as a function of temperature at standard pressure. Understanding the chosen standard state of gases, especially unstable compounds and ions, requires knowledge of chemical thermodynamics, since in this case the numerical values refer to a highly idealized state.
Let us look at a fragment of the JANAF table with the thermodynamic properties of oxygen:
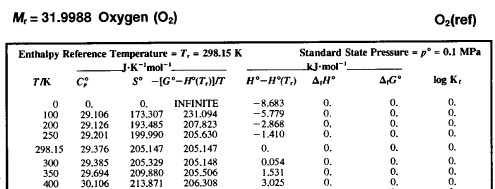
Molar values are given; molar mass is given separately. The superscript º indicates that the thermodynamic properties are given at standard pressure (1 bar). Using the thermal equation of state, the data can be converted to other pressures. The enthalpies of formation and the Gibbs energy of formation are zeros because oxygen is the standard simple substance.
The enthalpy column shows the difference in enthalpy at the current temperature relative to the enthalpy at 298.15 K. However, the entropy column shows absolute entropy – according to the third law of thermodynamics, the entropy of a substance at 0 K is zero. The column between entropies and enthalpies (often denoted as Φ) facilitates the calculation of the standard Gibbs energy of a chemical reaction:
∆ r G º(T) = ∆ r H (298.15 K) + ∆ r [ H (T) − H (298.15 K)] − T ∆ r S
∆ r G º(T) = ∆ r H (298.15 K) − T ∆ r Φ
The computer representation of the database stores only the Gibbs energy polynomial, since all other thermodynamic properties are found as its derivatives. Let me emphasize the mathematical equivalence of functions U(S, V) and G(T, p) to represent the thermodynamic properties of a substance. In both cases, the derivatives yield all other thermodynamic properties; these functions in terms of independent variables are therefore called fundamental functions.
The difference lies in the independent variables, since solving problems in chemical thermodynamics typically requires thermodynamic properties at given temperature and pressure. In the case of the Gibbs energy, calculations follow directly, while in the case of the internal energy, an internal mathematical problem must first be solved to find the necessary values of the independent variables that correspond to the given temperature and pressure. Thus, the use of Gibbs energy in practice is associated with the choice of convenient variables for solving practical problems.
In Chapter 5 ‘Adiabatic Flame Temperature‘ there are two examples that demonstrate the use of thermodynamic tables.
Next: Chapter 4. Clausius Inequality as Equilibrium Criterion
References
NIST-JANAF Thermochemical Tables, Fourth Edition, Monograph No. 9, Journal of Physical and Chemical Reference Data, 1998.
Thermodynamic Properties of Individual Substances (In Russian). In four volumes, third edition, 1978–1982.
Additional information
In Russian. Caloric equation of state: Gay-Lussac and Joule-Thomson experiments: History of the caloric equation of state. Dependence of internal energy on volume and enthalpy on pressure at constant temperature. The introduction of entropy allows one to calculate these derivatives from the thermal equation of state.
Discussion