The new version as the preprint
Szilard’s Demon: Information as a Physical Quantity? doi:10.20944/preprints202512.1224.v1
History of thermodynamics of information. Maxwell’s demon. Smoluchowski. Szilard. Brillouin, Bennett (Landauer’s principle) and Zurek. Critique of thermodynamics of information. Problem of coordination.
Also see my book translated in English ‘Understanding Entropy in Light of a Candle‘: Classical thermodynamics. Statistical mechanics. What does physics say? Physics, mathematics and the world.
Below I have left pieces that are not included in the preprint and in the book.
____
If I consider my personal area of expertise: thermodynamics and experimental thermodynamics, information as such is not there. A simple example. Below is the Fe-C phase diagram as computed according to the CALPHAD approach (picture is used to be on www.calphad.com). The thermodynamic entropy has been employed, the information concept not.
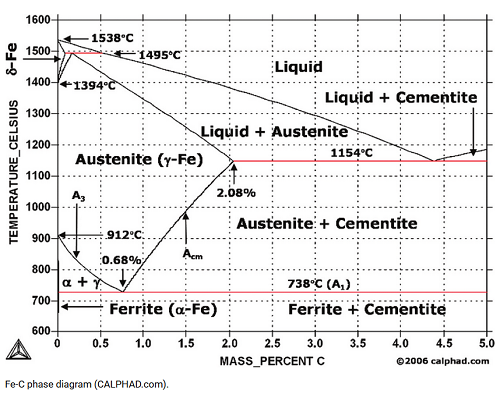
Hence we have an interesting situation. Everybody is convinced that the entropy is information but when we look at the thermodynamic research, the information is not there. How it could happen? As usual, a shoemaker has no shoes?
___
Alternatively one could say that the viewpoint “information and the entropy are the same” brings us useful conjectures. However, no one told me exactly what useful conjectures follow. In discussion on the biotaconv [5], I have suggested to consider two statements
- The thermodynamic and information entropies are equivalent.
- The thermodynamic and information entropies are completely different.
and have asked what the difference it makes in the artificial life research. I still do not know the answer.
___
I used to work in chemical thermodynamics for quite a while. No doubt, I have heard of the informational entropy but I have always thought that it has nothing to do with the entropy in chemical thermodynamics. Recently I have started reading papers on artificial life and it came to me as a complete surprise that so many people there consider that the thermodynamic entropy and the informational entropy are the same. Let me cite for example a few sentences from Christoph Adami “Introduction to Artificial Life”:
p. 94 “Entropy is a measure of the disorder present in a system, or alternatively, a measure of our lack of knowledge about this system.”
p. 96 “If an observer gains knowledge about the system and thus determines that a number of states that were previously deemed probable are in fact unlikely, the entropy of the system (which now has turned into a conditional entropy), is lowered, simply because the number of different possible states in the lower. (Note that such a change in uncertainty is usually due to a measurement).
p. 97 “Clearly, the entropy can also depend on what we consider “different”. For example, one may count states as different that differ by, at most, del_x in some observable x (for example, the color of a ball drawn from an ensemble of differently shaded balls in an urn). Such entropies are then called fine-grained (if del_x is small), or course-grained (if del_x is large) entropies.”
This is completely different entropy as compared with that used in chemical thermodynamics. The goal of this document is hence to demonstrate this fact.