Неравенства в классической термодинамике

Ранее: Обратимые процессы в классической термодинамике

Содержание: Термодинамика

Нередко при записи основного уравнения классической термодинамики

dU = TdS — pdV

говорится, что оно справедливо только для равновесных процессов, а при неравновесных следует использовать знак неравенства (основное неравенство). Правда в этом случае обычно не поясняется смысл входящих в соотношение величин и не дается пример, в котором показывается использование неравенства.

Этот вопрос будет разобран ниже — будет показано, как правильно записать неравенство, что оно означает, и будет приведен простой пример с его использованием. Начнем с рассматриваемой системы, поскольку требуется четкое понимание, к чему относятся рассматриваемые величины и приведенное основное уравнение. Рисунок из книги Сади Карно будет служить наглядной иллюстрацией:

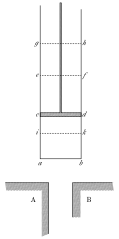
В цилиндре с поршнем находится так называемое рабочее тело, которое состоит из вещества с постоянной массой и составом. Обычно берется газ, но основное уравнение относится к любому веществу при рассмотрении закрытой термодинамической системы, в которой не происходят химические и фазовые реакции. В противном случае потребовалось бы расширение основного уравнения с включением химических потенциалов.

Кроме цилиндра на рисунке показаны два тела А и В, которые играют роль источников теплоты при разных температурах. С точки зрения настоящего рассмотрения я буду называть их терморегуляторами, поскольку они задают определенные температуры. Таким образом, поршень и терморегулятор играют роль внешних условий, поршень задает внешнее давление, а терморегулятор внешнюю температуру.

Вернемся к веществу рабочего тела — для последующего рассмотрения важно отделить состояние рабочего тела от внешних условий, задаваемых давлением вне поршня и температурой терморегулятора. Внешним условиям противопоставляется пространство состояний рабочего тела, обычно изображаемого в координатах давление — объем. Рассмотрим этот вопрос подробнее, поскольку отличие состояния рабочего тела от внешних условий будет ключевым для настоящего рассмотрения.

Согласно основному уравнению вещество рабочего тела имеет пять функций состояния: внутреннюю энергию (U), энтропию (S), объем (V), температуру (T, в абсолютной шкале температур) и давление (p). Технический термин функция состояния подчеркивает, что вещество обладает свойствами, которые в данном состоянии зависят только от этого состояния и не зависят от пути перехода в это состояние.

Пять физических величин (свойств) связаны между собой тремя уравнениями и поэтому только две из них независимы. В основном уравнении в качестве таковых выступают энтропия и объем, поэтому оно задает еще три уравнения связи: U(S, V), T(S, V) и p(S, V). Следует помнить, что температура и давление в этом уравнении являются первыми производными внутренней энергии и поэтому также являются функциями энтропии и давления.

Энтропию сложно использовать в качестве независимой переменной, но посредством математических преобразований можно сделать замену переменных и выбрать любые две физические величины из этих пяти как независимые переменные. Самое главное, состояние рабочего тела в принятых предположениях (постоянная масса и постоянный состав) задают две независимые переменные. Для текущего рассмотрения представим себе все возможные состояния рабочего тела в координатной плоскости температура — давление.

Следует обратить внимание, что температура и давления являются интенсивными свойствами и тем самым они отличаются от трех других величин. В неравновесном состоянии вещества возможны градиенты температуры и давления и тем самым для описания такого состояния потребуется введение температурного поля и поля давлений. Внутренняя энергия, энтропия и объем являются экстенсивными свойствами и можно говорить о их численных значениях даже в случае введения полей температуры и давления.

Вид основного уравнения термодинамики показывает, что оно не приспособлено для описания состояний с полями температуры и давления. Наличие температуры и давления рабочего тела в этом уравнении подразумевает однородность температуры и давления, то есть, отсутствие градиентов температуры и давления в рабочем теле. Поэтому введения знака неравенства непосредственно в это выражение ни к чему хорошему не приводит — использование основного неравенства для процессов с градиентами температуры и давления в рабочем теле в таком виде невозможно.

В то же время исходное основное уравнение термодинамики будет применимо во всех случаях при рассмотрении пространства состояний рабочего тела при однородных температурах и давлениях, независимо от того, каким способом был осуществлен переход из одного в другое состояние, поскольку в этом заключается весь смысл термина функции состояния. Рассмотрим сказанное на примере. Рабочее тело находится в начальном состоянии с однородной температурой и давлением, которое можно приготовить путем использования одного из терморегуляторов (исходная температура) и поршня (внешнее давление). Теперь резко изменим внешние условия, например, передвинем рабочее тело к другому терморегулятору с другой температурой и резко изменим внешнее давление.

Состояние рабочего тела станет неравновесным по отношению к новым внешним условиям и начнется самопроизвольный переход из начального состояния в конечное, который будет сопровождаться в том числе появлением градиента температуры и давления в рабочем теле. Интуитивно должно быть понятно, что процесс будет продолжаться до тех пор, пока давление и температура рабочего тела не сравняются с новыми внешними температурой и давлением; в конце такого процесса температура и давление снова станут однородными внутри рабочего тела. Таким образом, мы перешли из одного состояния рабочего тела (p₁, T₁) к состоянию (p_ex, T_ex), в котором температура и давление рабочего совпадают с температурой и давлением, задаваемыми внешними условиями.

Так вот, основное уравнение термодинамики позволяет рассчитать изменение всех термодинамических свойств в этом процессе. Формально интегрирование этого уравнения от первого состояния к конечному будет соответствовать так называемому равновесному процессу, в котором градиенты температуры и давления не образуются. В то же время понятие функции состояния позволяет утверждаеть, что изменение термодинамических свойств, рассчитанных таким образом, не зависит от пути перехода между двумя состояниями и тем самым оно совпадет с изменением термодинамических свойств в неравновесном процессе, описанном выше.

Важно понять, что основное уравнение не включает в себя критерий самопроизвольности процесса и критерий равновесия. Основное уравнение термодинамики является соотношением для расчета изменения термодинамических свойств (функций состояния) в пространстве состояний рабочего тела с однородными температурами и давлениями.

Теперь перейдем к рассмотрению появления знака неравенства при выводе основного неравенства. Первый закон термодинамики связывает изменение внутренней энергии с теплотой (Q) и работой (W):

dU = dQ + dW = dQ — p_exdV

Следует обратить внимание, что в общем случае работа рабочего тела вычисляется через внешнее давление на поршне (p_ex). Это необходимо в первую очередь при рассмотрении неравновесных процессов, когда возникает поле давлений в рабочем теле, как в представленном примере выше. Запись выше позволяет корректно вычислить работу, совершенную рабочим телом или над рабочим телом в этом случае.

Энтропия связана с теплотой по второму закону термодинамики:

Равновесный процесс	$$dS=\frac{dQ}{T}$$
Неравновесный процесс	$$dS>\frac{dQ}{T_{\mathrm{ex}}}$$

В случае неравновесного процесса в неравенстве стоит не температура рабочего тела, а температура окружения (T_ex), в нашем случае терморегулятора. Именно это обстоятельство позволяет включить в рассмотрение неравновесные процессы в рабочем теле в случае возникновения градиентов температуры в рассматриваемом примере.

Важно отметить, что термодинамическое неравенство относится к величине, которое не является функцией состояния — выше это теплота (также работа не является функцией состояния). Таким обраом неравенство относится к теплоте, а не к энтропии. В рассматриваемом примере изменение энтропии рабочего тела в равновесном и неравновесном процессе будет одно и то же; неравенство выше говорит, что в этом случае отличие будет в теплоте, связанной с разными процессами.

Таким образом при соединении неравенства из второго закона с первым законом заключительное основное неравенство будет выглядеть таким образом:

dU < T_exdS — p_exdV

В неравенство входит внешние температура и давление, которые фиксированы и не являются функциями энтропии и объема. Именно это обстоятельство приводит к тому, что полученное правильным образом основное неравенство существенно отличается по смыслу от основного уравнения термодинамики, приведенного в начале заметки. При этом основное уравнение и основное неравенство играют разную роль в классической термодинамике. Основное уравнение описывает изменение термодинамических свойств рабочего тела в пространстве состояний, а основное неравенство является критерием самопроизвольности процесса в ходе достижения равновесия при заданных внешних условиях.

Для рассмотрения описанного выше примера перехода рабочего тела из одного состояния в конечное, связанное с задаваемыми внешними условиями удобно перенести все слагаемые в левую часть неравенства:

dU — T_exdS + p_exdV < 0

Это задает функцию, которая в самопроизвольном процессе может только уменьшаться и которая при достижении конечного равновесного состояния будет минимальна. Таким образом критерий самопроизвольного процесса одновременно является критерием достижения конечного равновесного состояния (минимальное значение функции в левой части неравенства).

В классической термодинамике в конечном равновесном состоянии всегда получается однородные температура и давления, когда все градиенты исчезают. Поля температуры и давления появляются в неявном виде при использовании вариационного исчисления при поиске минимум функции выше. Поэтому я упрощу задачу и при рассмотрении неравенства выше я ограничу рассмотрение состояниями рабочего тела с однородными температурой и давлением. Задача станет такой — при рассмотрении всех возможных состояния рабочего тела с однородными температурами и давлениями найти равновесное состояние, которое соответствует заданным условиям. Интуитивно ответ понятен, но давайте увидим формально, что неравенство выше согласуется с интуитивными ожиданиями — что его применение приводит к установлению термического и механического равновесия.

В рассматриваемой задаче при заданных ограничениях можно заменить dU в неравенстве выше на выражение из основного уравнения из начала заметки. Это дает следующее выражение

(T — T_ex)dS + (p_ex — p)dV < 0

Теперь должно стать понятнее, что минимум функции слева будет достигаться при достижении рабочим телом температуры и давления, равным внешним давлению и температуры, то есть, неравенство является критерием термического и механического равновесия. Для наглядности сделаю ниже вычисление левой части в случае одного моля идеального газа: pV = RT (R — универсальная газовая постоянная). Для удобства переведу неравенство в пространство состояний температура — объем, поскольку в этих переменных получаются наиболее простые выражения для расчета. Для этого использую выражение энтропии как функцию от этих независимых переменных:

$$dS=\frac{C_V}{T}dT+{\left(\frac{\partial p}{\partial T}\right)}_{V}dV=\frac{C_V}{T}dT+\frac{R}{V}dV$$

Первая часть уравнения относится к любому телу; C_V — теплоемкость при постоянном объеме, которая ниже будет считаться независимой от температуры. Это уравнение является следствием того, что основное уравнение объединяет пять физических величин, среди которых есть только две независимые. Тем самым есть внутренние связи между этими величинами, которые можно использовать для преобразования переменных. При этом не требуется никаких других законов, вся необходимая информация для преобразования содержится в основном уравнении термодинамики в начале заметки. Вторая часть уравнения получена вычислением производной по уравнению состояния идеального газа. Подстановка в неравенство плюс использование уравнения состояния идеального газа плюс выкладки приводит к выражению неравенства в случае одного моля идеального газа:

$$\left(T—T_{ex}\right)\frac{C_V}{T}dT+\left(\frac{R{T}_{ex}}{V_{ex}}—\frac{R{T}_{ex}}{V}\right)dV<0$$

Поскольку переменные оказываются разделенными, можно взять интеграл при переходе из состояния (V₁, T₁) в (V₂, T₂), что дает конечное расчетное выражение:

$$C_V\left(T_2—T_1\right)—T_{ex}{C}_{V}ln\frac{T_2}{T_1}+\frac{R{T}_{ex}}{V_{ex}}\left(V_2—V_1\right)—{RT}_{ex}ln\frac{V_2}{V_1}<0$$

В этом выражении (V₁, T₁) относятся к начальному состоянию в примере, (V_ex, T_ex) — к внешним условия, (V₂, T₂) является промежуточным состоянием. Неравенство говорит, какие промежуточные состояния допустимы с точки зрения законов термодинамики при переходе из (V₁, T₁) в (V_ex, T_ex), а также в каком случае достигается минимум функции слева. Напомню, что минимиальное значение функции будет соответствовать равновесному состоянию относительно заданных внешинх условий (V_ex, T_ex). Ниже представлен контурный график для функции в левой части неравенства для двух фиксированных точек (V₁, T₁) и (V_ex, T_ex) как функция промежуточного состояния (V₂, T₂):

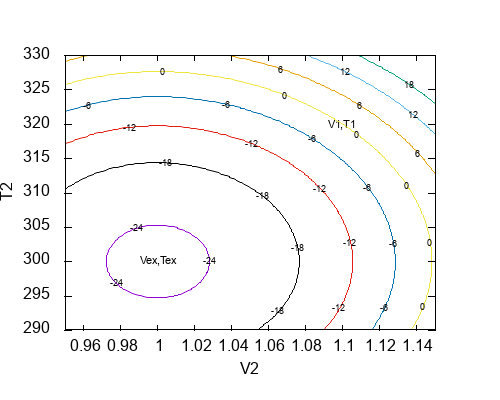
Как и следовало ожидать, функция достигает минимума в (V_ex, T_ex), это будет конечным равновесным состояниям. Положительные значения неравенства показывают, что в данных условиях самопроизвольный переход из (V₁, T₁) в эту область термодинамически невозможен. Рабочее тело может самопроизвольно переходить только в сторону уменьшения функции в левой части неравенства. В то же время неравенство не позволяет вычислить путь перехода, а также оно не содержит информации о времени перехода. Неравенство только позволяет классифицировать возможные состояния при переходе из (V₁, T₁) в (V_ex, T_ex) на термодинамически допустимые и термодинамически недопустимые, а также оно говорит, что минимальное значение соответствует равновесному состоянию.

В заключение еще раз отмечу, что основное уравнение и правильным образом полученное основное неравенство играют разные роли в построении термодинамики и их объединение вместе в одно выражение не имеет смысла.

Далее: Законы термодинамики. Простейший пример тепловой смерти

Сценарий Gnuplot для построения графика

set nokey
set terminal png enhanced size 500,400
set output 'inequality_map.png'
set style textbox noborder
set view map scale 1
set isosamples 200, 200
unset surface
set contour base
set cntrlabel format '%8.3g' font ',7' start 20 interval 50 
set cntrparam levels incremental -24, 6, 18
set style data lines
R = 8.314
Vex = 1
Tex = 300
Cv = 2.5*R
V1 = 1.1
T1 = 320
fun(V2, T2) = Cv*(T2-T1)-Tex*Cv*log(T2/T1)+R*Tex/Vex*(V2-V1)-R*Tex*log(V2/V1)
set label "Vex,Tex" at Vex, Tex center font ',8'
set label "V1,T1" at V1, T1 center font ',8'
set xlabel "V2" 
set xrange [ 0.95 : 1.15 ]
set ylabel "T2" 
set yrange [ 290 : 330 ]
splot fun(x, y) with lines, fun(x, y) with labels boxed

Обсуждение

https://evgeniirudnyi.livejournal.com/383832.html