Законы термодинамики. Простейший пример тепловой смерти

Ранее: Неравенства в классической термодинамике

Содержание: Термодинамика

Первый и второй законы термодинамики связывают теплоту Q и работу W, которые не являются функциями состояния, с двумя функциями состояния — внутренней энергией U и энтропией S. Рассмотрим рисунок из работы Сади Карно:

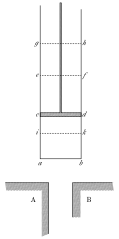
Рабочее тело может совершать механическую работу (передвижение поршня), а также обмениваться теплотой с окружением. Первый закон термодинамики вводит внутреннюю энергию тела:

$$dU=dQ+dW=dQ—pdV$$

Соглашение о знаке совершаемой работы сравнительно недавно поменялось и можно увидеть это уравнение с минусом перед работой; при переходе к выражению для механической работы расширения неоднозначность пропадает — в таком виде уравнение осталось без изменения.

Выражение второго закона для энтропии записывается по-разному для равновесных и неравновесных (самопроизвольных) процессов и это ведет к определенным трудностям при понимании:

Равновесный процесс	$$dS=\frac{dQ}{T}$$
Неравновесный процесс	$$dS>\frac{dQ}{T}$$

Понятие равновесного процесса было введено Сади Карно в качестве идеализации при вычислении максимального коэффициента полезного действия тепловой машины. Протекание реальных процессов приводит к меньшим значениям к.п.д. и именно это обстоятельство приводит к появлению неравенства. Следует отметить, что до введения термина энтропия Рудольф Клаузиус использовал понятие ‘приведенная теплота’ — это соответствует уравнению выше.

Ниже будет рассмотрен простой пример с использованием законов термодинамики — достижение теплового равновесия в изолированной системе (эквивалент тепловой смерти). Он покажет, каким образом неравенство выше используется на практике и тем самым раскроет смысл такой записи.

Важно отметить, что знак неравенства относится не к энтропии как таковой, а к теплоте. Энтропия является функцией состояния и поэтому ее всегда можно рассчитать как разницу энтропий двух состояний S₂ — S₁, вне зависимости от того, каким образом происходил переход между состояниями.

С математической точки зрения обратная температура, выраженная в абсолютной шкале температур, является интегрирующим множителем который делает из неполного дифференциала теплоты полный дифференциал энтропии. Поэтому второй закон термодинамики можно также рассматривать как способ введения абсолютной шкалы температур. Можно показать, что введенная таким образом абсолютная температура согласуется с абсолютной температурой в уравнении состояния идеального газа (для одного моля pV = RT).

Математические преобразования, которые я опущу, позволяют получить рабочие выражения для нахождения изменения внутренней энергии и энтропии как функции температуры и объема U(T, V) и S(T, V):

$$dU=C_{V}dT+\left[T{\left(\frac{\partial p}{\partial T}\right)}_V—p\right]dV$$ $$dS=\frac{C_V}{T}dT+{\left(\frac{\partial p}{\partial T}\right)}_{V}dV$$

Для расчета обоих функций, внутренней энергии и энтропии, достаточно данных по теплоемкости и термического уравнения состояния. Еще раз следует обратить внимания, что в обоих уравнениях нет и не может быть неравенств — интеграл функции состояния не зависит от пути интегрирования. Более того, третий закон термодинамики позволяет определить абсолютную энтропию. Энтропия любого тела равна нулю при нуле Кельвина, поэтому интеграл от нуля Кельвина позволяет рассчитать абсолютную энтропию тела.

Теперь можно вернуться к неравенству, которое переводится в утверждение, что энтропия изолированной системы (V = const и U = const) при протекании неравновесных (самопроизвольных) процессов возрастает:

$${\left(dS\right)}_{U,V}\ge 0$$

Рост энтропии изолированной системы продолжается до достижения равновесного состояния, когда значение энтропии достигает максимума. Это открывает возможность проведения расчета равновесного состояния. Рассмотрим это на простейшем примере, когда изолированная система состоит из двух подсистем, с одинаковой теплоемкостью (C_V,1 = C_V,2) и отделенных друг от друга неподвижной перегородкой — индекс 0 характеризует начальные значения температур:

$$T_{1,0}\mid T_{2,0}$$

Объемы подсистем таким образом не меняются и единственная возможность изменений связана с температурами — перегородка пропускает теплоту. Примем, что переход внутренней энергии в виде теплоты происходит таким образом, что в обоих подсистемах не возникает градиентов температур. Такое предположение соответствует нахождению обоих подсистем в состоянии локального равновесия.

Полная система с другой стороны не находится в состоянии равновесия, поскольку возможен обмен энергией между подсистемами. Задачей становится рассмотрение всех возможных состояний полной системы. По условию задачи изменения внутренней энергии подсистем должны быть равны между собой с обратным знаком (полная энергия сохраняется: U = U₁ + U₂ = const), что в случае одинаковых теплоемкостей приводит к простому соотношению между температурами:

$$d{U}_1=—d{U}_2$$ $$C_{V}d{T}_1=—C_{V}d{T}_2$$ $$T_1=T_{1,0}+x\mid T_2=T_{2,0}—x$$

Переменная x показывает возможные изменения температур, повышение температуры в одной подсистеме равно понижению температуры в другой. Суммарная внутренняя энергия от x не зависит, поскольку постоянство суммарной внутренней энергии заложено в вывод последнего соотношения.

В то же время суммарная энтропия зависит от значений текущих температур в подсистемах, то есть, от значения x. В уравнении ниже взят интеграл энтропии при изменении температуры, а S₀ обозначает суммарную энтропию в начальном состоянии:

$$S=S_1+S_2=S_0+C_{V}ln\frac{T_1}{T_{1,0}}+C_{V}ln\frac{T_2}{T_{2,0}}$$ $$S=S_0+C_{V}ln\frac{T_{1,0}+x}{T_{1,0}}+C_{V}ln\frac{T_{2,0}—x}{T_{2,0}}$$

Перед последним шагом рассмотрим график функции зависимости суммарной энтропии от x. Он построен для случая начальных температур 300 К и 400 К, при этом S₀=0, C_V=1.

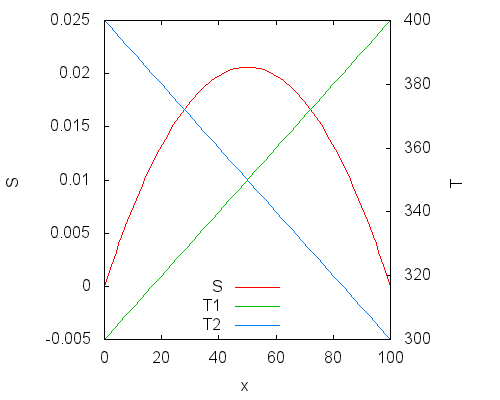
Изменение температуры показано на правой оси ординат: T₁ = 300 + x, T₂ = 400 — x, изменение энтропии на левой. Энтропия достигает максимума при x = 50, когда температуры подсистем становятся равными. Это согласуется с ожиданиями — равновесное состояние всей системы соответствует термическому равновесию между подсистемами.

Максимум энтропии соответствует равенству нулю производной энтропии, это позволяет получить ответ в общем виде:

$$dS/dx=0,x=\left(T_{2,0}—T_{1,0}\right)/2$$ $$T_{2,eq}=T_{1,eq}=\left(T_{2,0}+T_{1,0}\right)/2$$

Пример выше показывает, как можно использовать энтропию изолированной системы для расчета равновесного состояния. Пример также показывает, что из неравенства во втором законе термодинамики следует невозможность самопроизвольного перехода внутренней энергии в виде теплоты от более горячего тела к более холодному. Важно отметить, что такое является следствием только второго закона термодинамики, поскольку такой процесс не нарушает первый закон. Именно поэтому изменение энтропии в изолированной системе ассоциируется со стрелой времени; можно сказать, что возрастание энтропии в изолированной системе задает направление самопроизвольных процессов.

На языке тепловых машин неравенство отражает несимметричность работы и теплоты. Всю работу можно превратить в теплоту, но только часть теплоты можно превратить в работу. В этом случае в изолированной системе, которая включает в себя как тепловую машину, так и окружающие тела, постепенно теряется возможность совершения работы. Полная энергия сохраняется, но при достижении полного равновесия в изолированной системе теряется возможность совершения работы.

Рассмотренный пример допускает пессимистическое истолкование в виде так называемой тепловой смерти вселенной. Рудольф Клаузиус после введения энтропии не упустил возможность перенести сказанное на всю вселенную: ‘Die Energie der Welt ist konstant. Die Entropie der Welt strebt einem Maximum zu. (Энергия мира постоянна, энтропия мира стремится к максимуму)’. Это классический пример экстраполяционизма, когда результаты исследования тепловой машины без промедления и колебаний переносятся на весь мир.

Следует сразу же сказать, что в классической и статистической термодинамики полностью игнорируется силы гравитации, поэтому перенос результатов на всю вселенную следует рассматривать как метафору. Я не хочу сказать, что метафора неправильная, например, лорд Байрон еще в 1816 году до создания термодинамики в стихотворении Тьма живо описал процесс вымирания человечества без поступления энергии Солнца — см. Лорд Байрон о тепловой смерти (в конце заметки по приведенной ссылке). Тем не менее, ни классическая, ни статистическая термодинамика не позволяет рассчитать энтропию вселенной; для этого требуется коренное изменение формализма — про это нельзя забывать при обсуждении космологии.

Более правильная метафора тепловой смерти на базе обычной термодинамики — это теплоизолированный и закрытый бункер. Нельзя забывать, что возрастание энтропии в обычной термодинамике связано только с изолированной системой, то есть, с таким бункером. Должно быть понятно, что помещение живого в такой бункер с течением времени приведет к смерти. Также должно быть понятно, что воображаемые антиэнтропийные механизмы в биологии не помогут избежать смерти в таком бункере. В этом основная проблема разговоров про энтропию на популярном уровне — метафоры порядка и беспорядка, происходящие впрочем от самих физиков, ведут к неправильному восприятию понятия энтропии биологами и гуманитариями.

Далее: Замерзание переохлажденной воды

Приложение

Сценарий Gnuplot для построения графика:

set terminal png enhanced size 500,400
set output 'fig1.png'
set xlabel 'x'
set ylabel 'S'
set y2label 'T'
set y2tics
set ytics nomirror
set key center bottom
plot [x=0:100] log((300+x)/300)+log((400-x)/400) title 'S', 300+x axis x1y2 title 'T1', 400-x axis x1y2 title 'T2'

Обсуждение

https://evgeniirudnyi.livejournal.com/344794.html