Термодинамика обычно начинается с уравнения состояния идеального газа, но термодинамика нисколько не ограничена идеальным газом. В этой заметке рассмотрим термическое уравнение состояния V(T, p) в общем виде. Это позволит в том числе сформулировать минимальные требования к знанию математики при понимании классической термодинамики — математический анализ функции двух переменных. На этом уровне математики в дальнейшем можно понять смысл энтропии на уровне уравнений классической термодинамики без использования языка метафор и аналогий.
Начнем рассмотрение с рисунка из работы Сади Карно, который хорошо передает свойства системы, которая будет рассматриваться в этой и последующих заметках:
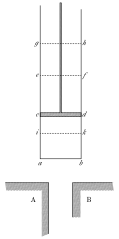
Рабочее тело состоит из вещества (рабочего тела), при этом система является закрытой и масса вещества остается неизменной. Предполагается, что вещество изотропно (газ или жидкость); есть три взаимосвязанных свойства — температура (ниже в абсолютной шкале температур), давление и объем. В принципе можно распространить рассмотрение на твердые вещества, но это требует введения в рассмотрение тензора напряжений, что усложнит рассмотрение.
Использование поршня и теплообмена (либо с нагревателем, либо с охладителем) меняет текущее состояния вещества на новое. Термическое уравнение состояния можно выразить разными способами: V(T, p), p(T, V) или T(V, p). Математически это три разные функции, но говорится, что они являются выражением одного уравнения состояния, поскольку они могут быть преобразованы друг в друга. В термодинамике единственное ограничение на термическое уравнение связано с условием устойчивости, что пока можно временно проигнорировать.
Использование термодинамики предполагает знание термического уравнения состояния, то есть, наличия экспериментальных данных. Проведение экспериментов связано с введением понятия термических коэффициентов, по сути дела производных уравнения состояния. Рассмотрим дифференциал объема V(T, p):
Две частные производные показывают зависимость объема от изменения температуры и давления соответственно. Важно отметить, что при изменении состояния вещества на рисунке выше считается, что давление как и температура одинаково во всех частях вещества. Другими словами, рассматривается переход из одного равновесного состояния в другое.
Уравнение выше также показывает важную особенность, про которую нельзя забывать — в уравнениях термодинамики отсутствует время. При изменении состояния вещества строго говоря вначале возникают градиенты температуры и давления (поле температур и поле давлений), но далее через некоторое время система приходит в состояние равновесия — значение давления и температуры выравниваются и становятся одинаковыми в любой точке вещества.
Существуют кинетические уравнения, которые позволяют рассчитать время достижения равновесия, в самой термодинамике рассматривается только связь между равновесными состояниями. В этом случае говорится о равновесной термодинамике и некоторые даже предлагают заменить название термодинамика на термостатика. Однако нельзя забывать, что даже в равновесной термодинамике остается динамика превращения теплоты в работу или работы в теплоту.
Для удобства производные нормируются, что дает следующие термические коэффициенты:
| Коэффициент объемного расширения | |
| Изотермический коэффициент сжатия | |
| Относительный коэффициент давления |
Важно отметить, что при нормировке обычно используются фиксированные значения объема и давления (V0 и p0), но это строго не оговаривается в определениях термических коэффициентов. Следует обратить на это обстоятельство внимание при использовании табличных данных.
В целом три варианта термического уравнения состояния должны привести к шести производным и тем самым к шести термическим коэффициентам. Между ними существует связь, которую накладывает математика. Кстати, решения многих задач в термодинамике сводится к поиску связи между разными производными и в данном случае требуется знание уравнений из математического анализа.
В данном случае используется связь между частными производными двух функций y(x,z) и x(y,z), которые получаются преобразованием друг из друга — для краткости это соотношение будет называться инвертером:
Это уравнение позволяет из трех термических коэффициентов выше найти три недостающие термические коэффициента — следует просто взять обратные величины.
Более того, есть только два независимых термических коэффициента в силу еще одного соотношения — для краткости оно будет называться пермутером:
Использование пермутера вместе с инвертером позволяет найти связь между тремя термическими коэффициентами выше:
Представим себе, что были проведены три независимых эксперимента по измерению трех термических коэффициентов. Математика, следующая из предположения о существовании термического уравнения состояния, требует, чтобы между ними выполнялось уравнение выше. Если эксперименты показывает отличие, выходящее за пределы ошибок измерения, то следует проверить условия проведения экспериментов. Возможно, что где-то что-то пошло не так. Если же разница остается, то по всей видимости это означает, что в рассматриваемом объекте требуется введение дополнительных переменных — трех переменных не хватает.
Связи между термическими коэффициентами не ограничивается вышесказанным. Для перехода к следующему шагу требуется вспомнить, что термические коэффициенты (производные) на самом деле являются функциями — их можно рассматривать постоянными только при небольшом отклонении от измеряемого состояния. Вторую смешанную производную функции можно образовать двумя способами, значение же смешанной производной не зависит от порядка дифференцирования. На примере дифференцируемой функция z(x,y):
Для наглядности выпишу дифференциал dz в виде, где первые производные обозначены как функции f1 и f2:
Тогда равенство смешанных производных будет выглядеть таким образом:
Две производные (два термических коэффициента) в целом независимы — из одной нельзя получить вторую. Но между их функциональными зависимостями есть определенная связь в силу независимости смешанной производной от порядка дифференцирования.
В заключение следует отметить, что в математике на уровне дифференциалов двух переменных появляются объекты, для которых последнее равенство не выполняется. В этом случае говорят о неполном дифференциале, которому нельзя поставить в соответствие функцию состояния. Неполный дифференциал можно проинтегрировать, но интеграл будет зависеть от пути интегрирования, а также интеграл по замкнутому контуру не будет равен нулю. В термодинамике к таким объектам относится теплота и работа. Последнее уравнение можно рассматривать как критерий по которому можно определить, является ли дифференциал полным или нет.
Далее: Законы термодинамики. Простейший пример тепловой смерти