Ранее: Часть 1. Классическая термодинамика
Температура оказалось первой немеханической физической величиной, которая тем не менее важна для всех теорий механики сплошных сред. Эрнст Мах при рассмотрении истории термодинамики в книге ‘Принципы теории теплоты‘ отдает приоритет в формальном введении температуры Джеймсу Максвеллу (1871 год); по всей видимости до Максвелла такое утверждение считалось очевидным. Определение Максвелла соответствует так называемому нулевому закону термодинамики, который обычно связывают с Фаулером и Гугенгеймом (1939 год).
Мы начнем с определения Максвелла, а затем перейдем к более общему понятию термического уравнения состояния, которое лежит в основе термометрии. Картинка Сади Карно позволяет дать наглядное представление необходимой мысленной модели и одновременно обсудить понятие идеального жидкостного и газового термометра. Далее рассмотрим историю термометрии. Интересно отметить, что большие погрешности измерений в начальный период сыграли полезную роль в формировании уравнения состояния идеального газа, которое в настоящее время лежит в основе температурной шкалы.
Утверждение о наличии термического уравнения состояния кажется примитивным: f(t, V, p) = 0, но эта простая математическая формулировка содержит в себе следствия, важные для экспериментальных исследований. Их рассмотрение одновременно показывает требования к уровню минимально необходимой математики при обсуждении классической термодинамики. В последнем разделе будет затронута роль понятие температурного поля, играющего важную роль во многих теориях механики сплошных сред и нулевого закона в построении термодинамики.
- Максвелл о температуре
- Термическое уравнение состояния
- Из истории термометрии
- Уравнение состояния идеального газа и абсолютная температурная шкала
- Математика термического уравнения состояния
- От температуры к температурному полю
Максвелл о температуре
Приведу перевод из русского издания книги Максвелла ‘Теория теплоты‘ 1888 года (он соответствует английскому тексту в первом издании 1871 года):
‘Определение температуры. — Температура тела есть его термическое состояние, рассматриваемое по отношении к способности сообщать теплоту другим телам.’
‘Определение высшей и низшей температуры. — Если два тела находятся в тепловом сообщении и одно из них теряет теплоту, а другое приобретает, то температура тела, теряющего теплоту, называется высшею, а температура тела, приобретающего теплоту, называется низшею температурою.’
‘Примечание. — Если ни одно из двух тел, находящихся в тепловом сообщении, не теряет и не приобретает теплоты, то температуры обоих тел называются равными. Оба тела называются тогда находящимися в тепловом равновесии.’
‘Закон равных температур. — Тела, температуры которых равны температуре одного и того же третьего тела, имеют равные температуры.’
Максвелл обобщает практику термометрии и дает формальное определение температуры. Важно отметить наличие двух частей в рассмотрении Максвелла. Закон равных температур вводит транзитивность температуры, а в определении высшей и низшей температуры содержится установление теплового равновесия. Без второго условия невозможно представить себе работу термометра — установление теплового равновесия является пререквизитом для введения практической температурной шкалы.
Правда, в определении температуры по Максвеллу присутствует теплота, что нарушает логику построения, поскольку до теплоты мы еще не дошли. Также температура в отличие от теплоты является характеристикой состояния вещества, теплота же характеризует изменение состояния вещества. Все сказанное Максвеллом справедливо, передача теплоты характеризует установление термического равновесия, но с точки зрения логики построения лучше убрать теплоту из определения температуры путем введения в рассмотрение термического уравнения состояния (ниже для краткости просто уравнение состояния).
Термическое уравнение состояния
Рассмотрим вновь рисунок из книги Сади Карно. Он будет хорошей визуализацией при рассмотрении уравнения состояния и тем самым поможет избавиться от теплоты в определении температуры Максвелла.
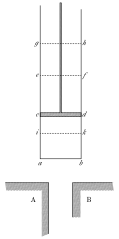
В этом разделе А и В будут телами, температура которых подлежит определению, а цилиндр с веществом под постоянным внешним давлением (поршень) будет играть роль термометра. Как уже упоминалось, предполагается, что физические величины объем (или высота вещества под поршнем) и давление уже известны, а также существуют методы измерения этих величин. Тогда введение теплового равновесия и температуры по Максвеллу для индивидуального вещества эквивалентно введению существования уравнения состояния: f(t, V, p) = 0, где t — практическая температура, шкалу измерения которой еще предстоит выбрать, V — объем, p — давление.
Подключение термометра к телу А приводит к установлению теплового равновесия и тем самым изменения температуры термометра. Согласно уравнению состояния это должно привести к изменению объема (высоты вещества под поршнем) при постоянном внешнем давлении: V(t, p). Объем вещества в термометре таким образом ставится мерой температуры, требуется только выбор шкалы изменений. Если перенос термометра от А к В не приводит к изменению объема, то из транзитивности температуры следует, что температура А и В одинаковы.
Сказанное не требует введения в рассмотрение теплоты, а также демонстрирует принцип работы газового и жидкостного термометра при постоянном давлении. Рисунок одновременно задает мысленную модель идеального измерительного прибора. Предполагается, что геометрия корпуса не меняется с изменением температуры (не происходит теплового расширения), а шкала температур привязана к выбранному внешнему давлению.
Обычно в качестве внешнего давления используется атмосферное давление, но оно несколько меняется. Этим изменением можно пренебречь в жидкостном термометре, но оно существенного для газового термометра постоянного давления. При увеличении точности измерений также потребуются поправки на тепловое расширение корпуса термометра.
Из истории термометрии
Интерес к количественному измерению температуры возник в 17-ом веке и первые термометры были газовыми. Галилей, Отто фон Герике, Санторио, Дреббель и др. внесли вклад в усовершенствование газового термометра, но затем работа в этом направлении остановилась. Пришло осознание, что газовый термометр одновременно является барометром; другими словами его показания зависят в том числе от давления. Отмечу, что в то время эксперименты с давлением воздуха только начинались и параллельно шла работа по разработке барометра как измерительного прибора.
В результате в качестве рабочего тела в термометрии стали использовать жидкость — спирт или ртуть. Один из первых термометров был изготовлен во Флорентийской академии (1641 г.), далее следует отметить работы Даленсе, Галлея, Гюйгенса, Гука, Ренальдини и др. Наибольшего успеха в технологии изготовлении надежных термометров достигли Фаренгейт и Реомюр (1740 г.). Для калибровки термометров применялись разные реперные точки и также использовались разные шкалы.
Отмечу проблему с реперной точкой, связанной с температурой кипения воды. Она зависит от давления и это было обнаружено достаточно быстро. Решение в данном случае достаточно простое — выбрать в качестве реперной точки температуру кипения воды при определенном давлении и вводить необходимые поправки при процедуре калибровки. В то же время следует упомянуть об еще одной серьезной проблеме тех лет — при фиксированном давлении температура кипения воды несколько менялась в зависимости от того, как проводился процесс кипения воды. Проблема была связана с перегревом воды и потребовались специальные исследования для понимания происходящего и нахождения условий для кипения воды без перегрева.
Другая проблема с жидкостными термометрами была связана с тем, что расширение жидкостей происходит неравномерно. Это обнаружилось путем сравнения спиртового и ртутного термометра между собой. Каждый из них калибровался по температурам замерзания и кипения воды, после чего шкала делилась на равные интервалы. Сделанные таким образом ртутный и спиртовой термометр показывали разные температуры в промежутке от нуля до ста градусов Цельсия. Причина отличия связана с непостоянством коэффициента термического расширения — он оказался функцией температуры. Специальные исследования показали, что расширение ртути более равномерно и для калибровки стал использовать ртутный термометр.
Тем не менее, необходимость выбора рабочего вещества термометра поднимала вопрос о температурной шкале, независимой от вещества, используемого в термометре. Так, ртуть имела ограничение, связанное с температурой замерзания и кипения. По мере становления термометрии эти пределы были достигнуты и стал вопрос, каким образом можно проводить измерения температуры ниже температуры замерзания и выше температуры кипения ртути. Таким образом в конце 18-ого — начале 19-ого века возобновился интерес к газовому термометру. К этому времени стали понятны принципы измерения давления, поэтому появилась надежда, что уравнение состояния газа позволит ввести универсальную температурную шкалу.
Уравнение состояния идеального газа и абсолютная температурная шкала
Параллельно со становлением методов измерения температуры и давления шло изучение уравнения состояния газа. Появился насос, который позволил изменять давление, а также было возможно регулировать температуру газа. В этом случае картинка Сади Карно выше получает другую интерпретацию — экспериментатор задает внешние условия (температуру и давление) и следит за изменением объема: V(t, p). Другой вариант — контроль внешних условий температуры и объема и измерение давления: p(t, V).
В самом начале был известен только один газ, воздух (в случае постоянства состава его поведение не отличается от индивидуального вещества). По мере открытия химиками других газов стали изучаться их уравнения состояния и в силу недостаточной точности измерения сложилось представление о существовании универсального уравнения состояния для всех газов. В современном виде:
pV = nR(t + a)
где n — это число молей (отношение массы к молекулярной массе), R — универсальная газовая постоянная, a — константа, значение которой зависит от выбора практической температурной шкалы.
Более точные измерения физика Анри Виктора Реньо в середине 19-ого века показали, что поведение разных газов несколько отличается друг от друга и от предполагаемого универсального уравнения состояния газа выше. В то же время было показано, что поведение газа при понижении давления стремится к универсальному состоянию, поэтому во второй половине 19-ого века появился термин ‘уравнение состояния идеального газа’. Молекулярно-кинетическая теории дает объяснение наблюдаемым эффектам — уравнение состояния идеального газа отвечает газу без взаимодействий между молекулами, что достигается при малых концентрациях (малых давлениях).
Несмотря на отличие уравнения состояния идеального газа от реальных газов именно оно стало использоваться для построения абсолютной температурной шкалы. Введение такой шкалы напрашивается уже из формы уравнения, поскольку при t = −a получается нулевой объем газа, и тем самым появляется мысль о введении абсолютной температуры: T = t + a.
Это получило обоснование в классической термодинамике и будет рассмотрено в следующей главе. Отношение функций температур практической шкалы связывается с максимальным коэффициентом полезного действия тепловой машины. При введении абсолютной температурной шкалы максимальный коэффициент полезного действия становится равным отношению температур, измеренных в этой шкале. Важно, что такая абсолютная температурная шкала совпадает с абсолютной температурой T в уравнении состояния идеального газа.
Отличие поведения реальных газов от уравнения состояния идеального газа приводит к необходимости введения поправок при использовании реальных газов в качестве рабочего тела термометра. Молекулярно-кинетическая теория подсказывает вид уравнения состояния для реальных простых газов и метрологи в конечном итоге могут использовать газовый термометр с реальными газами путем введения поправок на неидеальность поведения этих газов. Такова непростая работа метрологов, поправка поправку подгоняет, но в любом случае именно газовый термометр рассматривается как наиболее точное устройство для измерения температуры, а уравнение состояния несуществующего идеального газа служит основой для принятой температурной шкалы.
Математика термического уравнения состояния
Рассмотрим уравнение состояния в общем виде. Это позволит в том числе сформулировать минимальные требования к знанию математики при понимании классической термодинамики — математический анализ функции двух переменных. Для понимания последующего изложения требуется, как минимум, общее понимание записанных в этом разделе уравнений.
Уравнение состояния можно выразить тремя способами: V(T, p), p(T, V) или T(V, p). Формально это три разные функции, но они являются выражением одного уравнения состояния, поскольку они могут быть преобразованы друг в друга. Решение практических задач предполагает знание уравнения состояния, то есть, наличия экспериментальных данных. Проведение экспериментов связано с определением термических коэффициентов, по сути дела производных уравнения состояния.
В общем случае при изменении состояния вещества вначале возникают градиенты температуры и давления (поле температур и поле давлений), но далее через некоторое время система приходит в состояние равновесия — значение давления и температуры выравниваются и становятся однородными. Уравнение состояния относится только к конечным равновесным состояниям.
Рассмотрим дифференциал объема V(T, p):
Две частные производные показывают зависимость объема от изменения температуры и давления соответственно. В записанном уравнении отсутствует время, что подчеркивает вышесказанное обстоятельство — производные связывают между собой однородные равновесные состояния вещества.
Для удобства производные нормируются, что дает следующие термические коэффициенты:
| Коэффициент объемного расширения | |
| Изотермический коэффициент сжатия | |
| Относительный коэффициент давления |
При нормировке часто используются фиксированные значения объема и давления (V0 и p0), но это не оговаривается в определениях термических коэффициентов.
В целом три варианта уравнения состояния должны привести к шести производным и тем самым к шести термическим коэффициентам. Между ними существует связь, которая следует из математики. Рассмотрим две функции y(x, z) и x(y, z), которые получаются преобразованием друг из друга. Между частными производными этих функций существует связь — для краткости это соотношение будет называться инвертером:
Это уравнение позволяет из трех термических коэффициентов выше найти три недостающие термические коэффициента — следует просто взять обратные величины.
Более того, есть только два независимых термических коэффициента в силу еще одного соотношения для трех функций, x(y, z), y(x, z) и z(x, y), которые получаются преобразованием друг из друга. Для краткости оно будет называться пермутером:
Использование пермутера вместе с инвертером позволяет найти связь между тремя термическими коэффициентами выше:
Представим себе, что были проведены три независимых эксперимента по измерению трех термических коэффициентов. Математика, следующая из предположения о существовании термического уравнения состояния, требует, чтобы между ними выполнялось уравнение выше. Если эксперименты показывает отличие, выходящее за пределы ошибок измерения, то следует проверить условия проведения экспериментов. Возможно, что где-то что-то пошло не так. Если же разница остается, то по всей видимости это означает, что в рассматриваемом объекте требуется введение дополнительных переменных — трех переменных не хватает.
Связи между термическими коэффициентами не ограничивается вышесказанным. Для перехода к следующему шагу требуется указать, что термические коэффициенты (производные) на самом деле являются функциями — их можно рассматривать постоянными только при небольшом отклонении от измеряемого состояния. Вторую смешанную производную функции можно образовать двумя способами, значение же смешанной производной не зависит от порядка дифференцирования. На примере дифференцируемой функция z(x,y):
Для наглядности выпишу дифференциал dz в виде, где первые производные обозначены как функции f1 и f2:
Тогда равенство смешанных производных будет выглядеть таким образом:
Две производные (два термических коэффициента) в целом независимы — из одной нельзя получить вторую. Но между их функциональными зависимостями есть определенная связь в силу независимости смешанной производной от порядка дифференцирования.
В заключение скажу, что среди дифференциалов двух переменных в математике (предпоследнее уравнение выше) появляются объекты, для которых последнее равенство не выполняется. В этом случае говорят о неполном дифференциале, которому нельзя поставить в соответствие функцию состояния z(x,y). Неполный дифференциал можно проинтегрировать, но интеграл будет зависеть от пути интегрирования, а также интеграл по замкнутому контуру не будет равен нулю. Последнее уравнение можно рассматривать как критерий, по которому можно определить, является ли дифференциал полным или нет. В термодинамике к таким объектам относится теплота и работа — они не являются функциями состояния.
От температуры к температурному полю
Понятие температуры обобщается на случай градиента температур путем введения температурного поля, когда предполагается, что каждая точка сплошной среды имеют свою температуру, при этом температура меняется от точки к точке непрерывным образом. Примером является уравнение теплопроводности Фурье, в котором поле температур играет ключевую роль. Современная физика задает границы использования поля температур, характерную величину длины, переход за границу которой делает это понятие неприменимым.
В этом разделе рассмотрим вопрос измерения температуры в поле температур при условии, что размер термометра превышает характерную величину длины выше. Это само по себе на первый взгляд требует совмещение несовместимого — условие установления теплового равновесия накладывается на случай с наличием градиентов температуры, то есть, с отсутствием теплового равновесия.
Начнем с температуры на границе рассматриваемого температурного поля. Предположим, что рабочее тело на картинке Сади Карно подключено одновременно к двум термостатам А и В с разными температурами, которые прикладываются к разным сторонам тела. Внутри тела устанавливается градиент температур между двумя заданными температурами, но в этом случае нетрудно представить измерение температур термостатов.
Следующий шаг требует введения в рассмотрение небольшого термометра, поскольку жидкостный и газовый термометр слишком велики. Попытка их использования в температурном поле приведет к градиентам температуры внутри самого термометра. Поэтому рассмотрим термопару, термометр, работающий на принципе термоэлектрического эффекта. В идеальной модели термопары спай изображается точкой, но на самом деле он имеет вполне определенные размеры, превышающие минимальную характерную длину.
Использование термопары для измерения температуры в середине тела связано с несколькими проблемами. При подсоединении спая к телу существует термический контакт, подключение несколько меняет температурное распределение, а также в конечных размерах спая существует небольшой градиент температуры. В этом смысле схема идеального измерительного прибора становится формально недостижимой, но можно оценить дополнительные неопределенности и учесть их в погрешности измерений.
Рассмотрение выше опирается на представление о локальном тепловом равновесии между спаем и местом измерения температуры. Существует поле температур, но в области подключения термопары можно говорить о средней температуре, которая адекватно характеризует температуру в этой области. В таких рамках мысленную модель температурного поля в рамках перечисленных ограничений можно использовать при рассмотрении проводимых экспериментов.
В любом случае температура и градиенты температуры (температурное поле) входят в теории механики сплошных сред. Можно предположить, что это обстоятельство было одной из причин, почему в 19-ом веке не был введен термин нулевой закон термодинамики — температура принадлежала не только термодинамике, а всей механике сплошных сред. Фаулер и Гугенгейм при введения термина нулевой закон термодинамики в 1939 году по всей видимости забыли об том обстоятельстве.
В заключение еще один момент, который появится в следующих главах при рассмотрении построения термодинамики. Установление теплового равновесия закладывается изначально и оно будет необходимо даже при рассмотрении первого закона, в котором рассматривается переход из одного равновесного состояния в другое. Далее во втором законе вводится абсолютная шкала температур (T); второй закон дает возможность определить температуру как производную внутренней энергии по энтропии: T = (∂U/∂S)V, а в заключение второй закон позволяет доказать установление теплового равновесия из неравенства Клаузиуса. Таким образом, структура классической термодинамики для многих, в особенности для математиков, представляется не идеальной. При рассмотрении этого вопроса важно не забывать про локальное равновесие, про связь температуры с полем температур и с теориями механики сплошных сред.
Далее: Глава 2. От теории теплорода к термодинамике
Информация
При написании использованы заметки ниже; они содержат дополнительную информацию и ссылки на первичные источники.
Установление равновесия и минус первый закон термодинамики: Обсуждение статьи ‘Происхождение асимметрии во времени в термодинамике: Минус первый закон‘. Нулевой закон по Фаулеру и Гугенгейму, 1939. Определение температуры Максвеллом, 1871. Механика сплошных сред.
Температура, термометр и практическая температурная шкала: Рассмотрение вопросов ‘Что такое температура?‘ и ‘Что считается измерением температуры?‘ в контексте истории измерений температуры. Историческое развитие или сложившаяся теория разрывают герменевтический круг.
Хасок Чанг: Изобретение температуры: Четыре эпизода из истории термометрии — температура кипения воды, поиск правильной шкалы, выход за границы ртутного термометра, поиск теории. Анализ книги в рамках проблемы координации ван Фраассена.
Уравнение состояние идеального газа: Рассмотрена история становления уравнения состояния идеального газа. Уравнения приведены с использованием шкалы Цельсия — это соответствует виду уравнений, используемых в ходе истории.
Проблема координации. Температура как физическая величина: Математика, физика и измерение. Измерение температуры в настоящее время. История термометрии. Проблемы выбора рабочего вещества для термометра. Температура, теплота и термодинамическая шкала.