Ранее: Глава 1. Температура и термическое уравнение состояния
В этой главе будут рассмотрены основные события, которые привели к появлению величины теплоты (вторая половина 18-ого века), а затем к пониманию, что теплота и работа не являются функциями состояния и введению взамен функций состояния внутренней энергии и энтропии (вторая половина 19-ого века).
Большую роль в произошедшем сыграли паровые машины, которые появились уже в 18-ом веке; они будут рассмотрены в первом разделе ‘Паровые машины‘. Правда, в 18-ом веке становление величины теплоты и появление калориметрии не было связано с развитием паровых машин. Таким образом, второй раздел ‘Теплота и калориметрия‘ не будет связан с паровыми машинами. Сади Карно предложил теорию идеальной паровой машины в 1824 году и это послужило отправной точкой для появления классической термодинамики. Это развитие будет рассмотрено в третьем разделе ‘Основные этапы становления термодинамики‘.
Законы термодинамики появились при рассмотрении работы идеальной паровой машины по циклу Карно. Я не буду разбирать эти выкладки, а сразу же приведу выражения для первого и второго закона в дифференциальной форме в четвертом разделе ‘Первый и второй законы термодинамики‘ с разбором того, что потребуется для изложения в последующих главах. В последнем разделе ‘Равновесные и обратимые процессы‘ будут разобраны особенности идеализации, введенной Карно. Требуется понять связь интегралов от дифференциальной формы первого и второго закона с поведением веществ.
Основным препятствием для изучения термодинамики являются попытки получить наглядный ответ на вопрос ‘что такое энтропия’ сразу же при рассмотрении формулировки второго закона. Нередко это приводит к заявлениям о недостатках термодинамики, которые стараются исправить без изучения термодинамики. Я ограничусь примером картезианцев, которые сходу объявили силу притяжения Ньютона ‘оккультной силой’ и старались найти свое решение без изучения механики Ньютона — не следует брать с них пример.
Паровые машины
Начну с выразительной цитаты Сади Карно из его единственной работы 1824 года ‘Размышления о движущей силе огня и о машинах, способных развивать эту силу‘:
‘Железом и огнем, как известно, питаются и поддерживаются механические производства. В Англии, может быть, нет ни одного промышленного заведения, существование которого не было бы основано на употреблении этих двух агентов в их широком использовании. Отнять у Англии в настоящее время ее паровые машины — означало бы разом отнять у нее железо и уголь, отнять у нее все источники богатства, уничтожить все средства к процветанию, это означало бы уничтожить эту великую мощь. Уничтожение флота, который она считает своей главной опорой, было бы для нее менее гибельным.’
Первая паровая машина Ньюкомена стала использоваться для откачки воды в угольных шахтах в Англии с 1712 года. Эта конструкция осталась без изменения до нового усовершенствованного дизайна паровой машины Джеймса Уатта (1780-ые годы). Однако в 18-ом веке существование паровых машин не оказало влияние не становление понятия теплоты, поскольку в работе машины участвовало слишком много взаимосвязанных процессов:
- Сгорание угля (понятие энергетика химических реакций не существовало, при этом в ходу была теория флогистона);
- Испарение/кипение воды и конденсация пара (теории фазовых превращений не существовало);
- Пар выступал в качестве рабочего тела (свойства пара не были изучены);
- Нагревание и охлаждение цилиндра и котла (понятия теплоты, температуры, теплопроводности и теплоемкости находились лишь в становлении);
- Сопоставление количества сожженного угля с массой поднятой воды (понятия работа и энергия еще не сформировались, закон сохранения энергии отсутствовал).
С другой стороны, в 19-ом веке необходимые теории стали появляться; хотя технологии во многом еще продолжали разрабатываться благодаря интуиции и смекалке инженеров. Правда, в 19-ом веке связь между инженерами и учеными была гораздо более тесной, чем сейчас, а нередко один человек был одновременно инженером и ученым. Отмечу учебник по классической термодинамике Анри Пуанкаре (первое издание 1892 г), в котором есть глава, посвященная паровым машинам. В ней Пуанкаре показывает себя прекрасным инженером. Он профессионально рассматривает коэффициент полезного действия паровых машин с учетом всех стадий, разбирает вклад цикла Карно и анализирует возможности повышения эффективности всей паровой машины с точки зрения термодинамики.
Теплота и калориметрия
Понятие теплоты появилось в ходе опытов по смешению теплых и холодных жидкостей. Так, Георг Рихман в Санкт-Петербургской академии опубликовал правило для смешения горячих и холодных количеств воды в 1750 году:
где m1 и m2 обозначают массы смешиваемых частей воды, а t1 и t2 — их начальные температуры. Понятие теплоты появилось позже в работах Джозефа Блэка, Иоганна Вильке и других. Было показано, что правило Рихмана не работает при смешении горячей воды и холодной ртути, а также при смешении теплой воды и льда. Начнем с последнего, поскольку этот эффект более наглядно показывает, что выделение / поглощение теплоты может происходить при постоянной температуре. Эффект постоянства температуры при плавлении льда был замечен до Блэка, но именно он ввел в ход понятие скрытой теплоты, под этим понималась теплота фазового перехода. Далее было установлено, что скрытая теплота связана со всеми известными в то время фазовыми переходами.
Следующий шаг был связан с введением понятия теплоемкости тела. Разным жидкостям при смешении до достижения теплового равновесия требовалось разное количество тепла. Использование теплоемкостей позволило обобщить правило Рихмана на смешение любых тел:
где дополнительно введены удельные теплоемкости С1 и С2. В случае смешения воды они одинаковы и в этом случае получается правило Рихмана. В случае смешения ртути и воды они разные и без их использования невозможно описать наблюдаемые результаты.
Для практического использования уравнения выше была введена единица теплоты. Одна калория определялась как теплота, необходимая для нагревания одного грамма воды на один градус по Цельсию; таким образом удельная теплоемкость воды получалась равной единице. Принятая теплоемкость воды давала возможность для определения теплоемкостей других тел и скрытых теплот. Антуан Лавуазье и Пьер-Симон Лаплас предложили универсальную конструкцию калориметра в 1780 году (ледяной калориметр), который активно использовался для измерения теплоты в 19-ом веке, в том числе для определения теплоты, выделяющейся при сгорании веществ.
Идеальный измерительный прибор, соответствующий ледяному калориметру, представляет собой лед при температуре плавления льда, 0ºC, внутри которого происходит происходит процесс охлаждения вещества от исходной температуры до 0ºC. Количество теплоты равно удельной теплоте плавления льда умноженной на массы образовавшейся воды. Другой вариант — протекание реакции сгорания в сосуде внутри льда. В этом случае из массы образовавшейся воды получается теплота сгорания реакции. Есть много технических сложностей, в силу которых точность ледяного калориметра невелика, и в настоящее время используются другие приборы. Однако понимания калориметрии на уровне ледяного калориметра должно быть достаточно для нашего рассмотрения классической термодинамики.
Попытка привязать теплоту как физическую величину к калориметру соответствует теории теплорода, которая вошла в ход с работ Лавуазье и оставалась в силе в первой половине 19-ого века. Математически теория теплорода сводится к введению теплоты как функции состояния. В случае чистого вещества есть две независимые переменные и таким образом постулируется существование калорического уравнения состояния, например, в переменных температура и объем: Q(T, V). В этих рамках считается, что калориметрия измеряет изменение теплоты между двумя состояниями:
Q2 — Q1 = ΔQ
Но последующие исследования показали, что невозможно согласовать такую гипотезу с экспериментами — теплота не является функцией состояния. Запись ΔQ в современных учебниках и статьях является явной ошибкой. Необходимые эксперименты для такого заключения были проведены уже в начале 19-ого века (свободное расширение газа, Гей-Люссак, 1807 г.), но в силу отсутствия альтернатив теория теплорода осталась, а эксперимент Гей-Люссака был проигнорирован. Мы рассмотрим его в следующей главе.
Для сравнения — в механике в то время существовал принцип невозможности вечного двигателя, но энергия в современном понимании не сохранялась. Маятник под действием сил трения останавливался; тело, падающее на Землю, вначале набирало скорость и приобретало живую силу (эквивалент кинетической энергии в терминологии Лейбница), но затем после удара о Землю живая сила пропадала. Возможно, что это было одной из причин, почему в механике отсутствовала энергия как величина; она появилась только после появления формулировок первого закона термодинамики.
Основные этапы становления термодинамики
В ходе создания термодинамики участвовало много ученых, но я ограничусь минимальным количеством имен. Уильям Томсон в те времена еще не был лордом Кельвиным, поэтому он останется как Томсон.
Цикл Карно в рамках теории теплорода (Карно, Клапейрон, Томсон)
Сади Карно ввел теорию идеальной тепловой машины в 1824 году. Его дневники показывают, что он сомневался в правильности теории теплорода, но ничего другого не было. Поэтому в своей работе он обратился к аналогии с падением воды — теплота переходит от высокой к низкой температуре и своим падением она производит работу. Труд Карно остался незамеченным и только работа Бенуа Клапейрона в 1834 году привлекла внимание к идеям Карно.
Гений Сади Карно проявился в том, что он смог предложить модель идеальной тепловой машины, разработанной для удобства анализа, но при этом можно было сделать выводы о работе реальных тепловых машин. Карно опирался на принцип невозможности вечного двигателя. Это позволяет доказать, что 1) максимальный коэффициент полезного действия тепловой машины (к.п.д.) не зависит от вещества рабочего тела; 2) в реальных машинах к.п.д. будет меньше, чем в идеальной. Именно последнее обстоятельство в конечном итоге приводит к появлению неравенства для энтропии.
Для получения максимального к.п.д. следовало убрать все возможные потери, что в свою очередь привело к исчезновению времени в явном виде в термодинамическом обратимом процессе и его противопоставлению необратимому процессу. Этот вопрос будет рассмотрен отдельно.
Уильям Томсон был настолько вдохновлен результатом независимости максимального к.п.д. от рабочего тела, что в 1848 году он на основе работ Клапейрона / Карно предложил на основе теории теплорода абсолютную шкалу температур; кстати, в этой работе он не соглашался с возможностью превращения теплоты в работу.
Тепловой эквивалент работы (Майер, Джоуль, Гельмгольц)
В калориметрии была введена единица теплоты калория. В механике систематическое употребление термина работа появляется с 1826 года в статьях Жана-Виктора Понселе, например работа по подъему груза (m g h). В настоящее время единица работы названа в честь одного из участников событий того времени, Джеймса Джоуля, поэтому на современном языке требовалось найти соответствие между калорией и джоулем; современное значение 1 кал = 4.184 Дж.
Первым показал эквивалентность работы и теплоты врач Роберт Майер в 1842 году. Семейный пивовар Джеймс Джоуль с молодости проявлял интерес к науке и технике. Именно он провел первые эксперименты по измерению механического эквивалента теплоты в 1843 году. Джоуль в конце концов смог привлечь Томсона на свою сторону, что в свою очередь помогло обратить внимание других физиков к этой идее. Герман Гельмгольц в 1847 году опубликовал работу, в которой в общем виде подчеркивалась сохранение энергии (в современной формулировке) при проведении разных физических процессов.
Как уже упоминалось, понятие энергии еще не существовало. Поэтому во всех трех работах речь шла о сохранении силы. Возможно, что именно это обстоятельство вызывало сомнения других физиков. Так, работы Гельмгольца и Джоуля были отвергнуты научными журналами и они опубликовали свои работы за свой счет. Майер с трудом добился публикации в ‘Анналах химии и фармакологии‘, а далее также издавал книги за свой счет.
Законы термодинамики (Клаузиус и Томсон)
Основы современной классической термодинамики заложены работами Рудольфа Клаузиуса и Уильяма Томсона в период от 1850 до 1865 года, при этом основная роль принадлежит Клаузиусу. Были сформулированы два закона термодинамики, которые устанавливали существование двух функций состояния — внутренней энергии и энтропии. Параллельно было показано, что ни теплота, ни работа не являются функциями состояния.
Ранее мы рассмотрели, что для чистого вещества температура, давление и объем связаны между собой термическим уравнение состояния. Первый закон термодинамики вводит новую функцию состояния, внутреннюю энергию (U), с ней связывается калорическое уравнение состояния. Второй закон вводит функцию состояния энтропию (S), при этом оказывается что для ее определения достаточно имеющихся термического и калорического уравнений состояния. В то же время состоянию вещества нельзя приписать ни теплоту, ни работу. Они появляются в ходе перехода вещества из одного состояния в другое, но их нет в состоянии вещества.
Первый и второй законы термодинамики
Начнем рассмотрение со знакомого рисунка Карно:
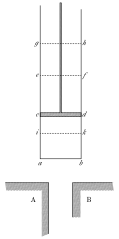
Идеализация Карно при нахождении максимального к.п.д требует, что температура и давление в веществе рабочего тела остаются однородными и в ходе процесса не возникают градиенты температуры и давления. Кроме этого тела А и В выступают в качестве идеальных источников теплоты — температура этих тел при теплообмене не меняется.
Идеальные процессы в цикле Карно называются равновесными (квазистатическими) или обратимыми процессами. Равновесный процесс обращает внимание только на состояние вещества рабочего тела, температура и давление остаются однородными в ходе процесса. Термин обратимый процесс требует большего, он включает в себя рассмотрение всей системы, включая идеальные источники теплоты А и В. Предполагается, что после совершения обратимого процесса в одну, а затем в обратную сторону, получается то же самое исходное состояние всей системы, включая состояния идеальных источников теплоты.
Должно быть понятно, что равновесные / обратимые процессы неосуществимы практически, потому что для движения поршня в ту или иную сторону требуется разница в давлении, а для теплообмена необходима разница температур. Это с неизбежность будет вести к возникновению градиентов температуры и давления в веществе рабочего тела. Такие процессы будут считаться неравновесными и доказывается, что в этом случае к.п.д. будет меньше максимального. Более подробно идеализация, связанная с введением равновесных и обратимых процессов, и трудности ее понимания будут рассмотрены в следующем разделе.
Первый закон термодинамики связывает изменение внутренней энергии с теплотой (Q) и работой (W). Согласно рекомендациям ИЮПАК теплота и работы считаются положительными, когда они увеличивают внутреннюю энергию вещества, поэтому в настоящее время первый закон выглядит таким образом:
dU = dQ + dW
В старых учебниках можно увидеть минус перед работой, поскольку ранее было другое соглашение о знаке работы. Этот минус в настоящее время ушел в выражение для работы:
dW = −pexdV
В общем случае работа рабочего тела вычисляется через внешнее давление на поршне (pex), поскольку в неравновесном процессе, внутри вещества рабочего тела возникает поле давлений. Запись выше позволяет корректно вычислить работу, совершенную рабочим телом или над рабочим телом в неравновесном процессе. В равновесном процессе давление над поршнем равно однородному давлению внутри вещества.
Дифференциалы теплоты и работы являются неполными и поэтому иногда их записывают несколько в другом виде, хотя с точки зрения математики это такие же бесконечно малые, как и другие дифференциалы. Отличие получается при интегрировании — интеграл зависит от пути интегрирования, поэтому значение интеграла нельзя записать как разницу начального и конечного состояния:
ΔU = Q + W
Также интеграл по замкнутому контуру для работы и теплоты не будет равен нулю в отличии от внутренней энергии:
0 = Q + W
Уравнение в таком виде соответствует завершению одного цикла Карно, когда состояние вещества рабочего тела пришло в исходное состояние. Внутренняя энергия есть функция состояния и поэтому разница равна нулю, состояние одно и то же — интеграл по замкнутому контуру для функции состояния обязан быть равным нулю. В то же время теплота превращается в работу или работа в теплоту — интеграл по замкнутому контуру для работы и теплоты не равен нулю, что еще раз подчеркивает невозможность записи знака Δ в этом случае.
Энтропия связана с теплотой по второму закону термодинамики:
| Обратимый процесс | |
| Необратимый процесс |
В этом случае важно состояние идеального источника тепла (тела А и В), поэтому говорится об обратимом и необратимом процессе. В случае необратимого процесса в неравенстве стоит температура идеального источника тепла (Tex). Именно это обстоятельство позволяет включить в рассмотрение необратимые процессы в рабочем теле в случае градиентов температуры.
Знак неравенства является источником многих вопросов и мы разберем это в следующих главах. Пока только отмечу, что знак неравенства относится не к энтропии, а к теплоте. Энтропия является функцией состояния, поэтому изменение энтропии от состояния 1 до состояния 2 является одним и тем же для обратимых и необратимых процессов.
Равновесные и обратимые процессы
Начну рассмотрение с выражения для максимальной работы, производимой рабочим телом (A = −W). Под интегралом стоит термическое уравнение состояния рабочего тела p(V, T), которое связывает внутренние давление (p) с температурой (T) и объемом (V):
Теперь требуется сформулировать необходимую идеализацию в виде мысленной модели, которая соответствует нахождению такого интеграла. При реальном движении поршня в рабочем теле возникают градиенты температуры и давления. В уравнение выше предполагается однородность давления и температуры в рабочем теле; таким образом первый шаг идеализации связан с пренебрежением градиентов температуры и давления. Это можно представить в виде очень медленного движения поршня, когда температура и давление рабочего тела остаются практически однородными.
Второй шаг идеализации связан с внешним давлением над поршнем, поскольку выражение для работы должно содержать именно это давление (pex). Приведенное выражение для максимальной работы требует, чтобы однородное давление рабочего тела в ходе процесса оставалось равным внешнему давлению. На первый взгляд возникает противоречие. С одной стороны, идеализация требует механического равновесия состояния рабочего тела (внутреннее давление равно внешнему давлению), с другой, протекание реального процесса требует отличия двух давлений; только в этом случае можно ожидать самопроизвольного передвижения поршня в сторону с меньшим давлением.
В этот момент вводится понятие квазистатического процесса, когда внешнее давление меняется небольшими порциями. Обычный образ связан с горой песка над поршнем; далее мы убираем или прибавляем песчинку в ходе процесса расширения или сжатия. Предельный переход получается при устремлении размера песчинки к бесконечно малому, что приводит нас к искомому интегралу выше, когда объем и давление рабочего тела связаны термическим уравнением состояния и когда в пределе внутреннее и внешнее давления равны между собой.
Обычное возражение сводится к тому, что такой предельный переход делает процесс невозможным, поскольку предполагается, что для перехода из одного равновесного состояния в другое требуется нарушение состояния равновесия. Однако этот аргумент смешивает мысленную модель с миром. Никто не спорит, что для протекания реального процесса требуется нарушить состояния равновесия. В то же время ничто не мешает вычислить интеграл выше и представить себе именно такое изменение в мысленной модели, соответствующей рисунку выше. В этом смысле равновесный процесс не есть самопроизвольный процесс, он не происходит сам по себе; равновесный процесс связывается с силой мысли, необходимой для взятия интеграла.
В случае изотермических процессов требуется дополнительно рассмотрение теплообмена, поскольку согласно первому закону термодинамики перемещение поршня связано с теплообменом (Q — количество теплоты, ΔU — изменение внутренней энергии):
В случае адиабатических процессов Q=0 (рабочее тело отключено от нагревателя или холодильника), в случае изотермических процессов с необходимостью Q≠0.
Вначале несколько слов про идеальный источник теплоты. Эти объекты также являются продуктами идеализации — требуется вообразить настолько большие объекты с заданными температурами, что отдача или прием энергии в виде теплоты не изменяет температуру этих объектов. Таким образом подсоединение рабочего тела к одному из этих объектов позволяет организовать изотермический процесс, когда несмотря на теплообмен температура нагревателя и соответственно рабочего тела не будет меняться.
В данной ситуации следует отметить, что не всякий квазистатический процесс является обратимым — для термодинамической обратимости требуется квазистатический процесс, но этого недостаточно. Понятие термодинамической обратимости включает в себя не только состояние рабочего тела, но и состояние всех остальных объектов в системе. Идея обратимого процесса в том, что исполнение цикла Карно вначале в одном направлении, а потом в противоположном должно привести все объекты в системе в исходное состояние.
Такое будет возможно, если температура рабочего тела в ходе изотермического процесса равна температуре нагревателя. Это обстоятельство связано с уравнением, связывающим количество теплоты и изменение энтропии в изотермическом процессе: Q = TΔS. Формально в этом уравнении должна стоять температура нагревателя и если она отличается от температуры тела, то это будет приводить к необратимому увеличению энтропии всей системы. С другой стороны, для теплообмена между нагревателем и рабочим телом в реальном мире требуется разность температур, поскольку теплота в самопроизвольном процессе передается только от более горячего к более холодному телу. Если два тела имеют одинаковые температуры, то они находятся в состоянии теплового равновесия и поток теплоты между ними равен нулю.
По сути дела при рассмотрении изотермического процесса требуется предельный переход, аналогичный таковому в случае внешнего давления. Следует начать с небольшой разницы температур, обеспечивающей передачу теплоты в нужном направлении, а потом устремить эту разницу к бесконечно малой величине. При переходе к нулю, когда в уравнении выше температура рабочего тела равняется температуре нагревателя в уравнении остается количество теплоты, необходимое для проведения изотермического процесса. Таким образом при рассмотрении обратимых процессов мы обязаны считать, что при изотермическом процессе происходит теплообмен между нагревателем и рабочим телом даже при равенстве температур между ними.
Напомню, что задача Карно состояла в нахождении выражения для максимального коэффициента полезного действия тепловой машины. Предельные переходы, рассмотренные выше, позволили решить эту задача. У реальных тепловых машин коэффициент полезного действия всегда будет меньше, а использование предельного перехода позволяет утверждать, что полученный таким образом к.п.д. является пределом, который получается при уменьшении потерь до нуля.
Рассмотрим в качестве примера маятник. Представление о невесомой нерастяжимой нити, а также замена тела материальной точкой приводит к простому уравнению движения мысленной модели, а устранение всех сил трения приводит к бесконечным колебаниям. В этом случае идеализации осуществляется в духе предельного перехода. Аналогичный переход совершил Карно при построении идеальной тепловой машины. Разница только в том, что предельный переход Карно приводит к отсутствию времени в конечных уравнения, поэтому для мысленного движения в обратимых процессах в цикле Карно требуется сила мысли для вычисления соответствующих интегралов.
Далее: Глава 3. Термодинамические свойства веществ
Информация
При написании использованы заметки ниже; они содержат дополнительную информацию и ссылки на первичные источники.
Теплота и калориметрия: История отделения понятия теплоты от понятия температуры. Правило Рихмана, скрытая теплота Блэка, теплоемкости тел. Калориметрия, термохимия и закон Гесса. Обсуждение результатов.
От паровой машины Ньюкомена к модели идеальной тепловой машины: В качества примера рассмотрен принцип работы паровой машины Ньюкомена. Приведены главные идеи Сади Карно, которые привели к созданию идеальной модели тепловой машины.
От теории теплорода к термодинамике: Теория теплорода и принцип невозможности вечного двигателя. Цикл Карно в рамках теории теплорода. Эквивалентность работы и теплоты. Первый и второй законы термодинамики.
Анри Пуанкаре: Термодинамика: Краткое содержание книги. Видение классической термодинамики того времени глазами известного физика. В конце выкладки с неполным дифференциалом теплоты dQ(V,p).
Обратимые процессы в классической термодинамике: Обратимые процессы как идеализация в духе предельного перехода. Рассмотрены мысленные модели в цикле Карно, соответствующие вычисляемым интегралах в изотермическом и адиабатическом процессах.