Ранее: Глава 2. От теории теплорода к термодинамике
Главной целью этой главы будет переход от первого и второго закона термодинамики к таблицах термодинамических свойств веществ. Термодинамика может быть использована для решения практических задач только при наличии свойств веществ, которые должны быть получены из специально проводимых экспериментов. Одновременно это дает представление о связи внутренней энергии и энтропии с экспериментами и тем самым будет ответом на проблему координации. Для краткости я проведу рассмотрение только с использованием калориметрии и использованием данных по термическому уравнению состояния, хотя существуют и другие эксперименты, результаты которых также используются при составлении термодинамических свойств индивидуальных веществ.
Мы начнем с рассмотрения калориметрии в разделе ‘Калориметр и функции состояния‘, а затем перейдем к объединенному уравнению первого и второго закона в разделе ‘Основное уравнение термодинамики‘. Функция внутренней энергии в переменных температуры и объема U(T, V) называется калорическим уравнением состояния. Для ее построения в дополнении к теплоемкостям требуются дополнительные эксперименты. Однако введение энтропии S(T, V) не только не требует новых экспериментальных данных, а даже позволяет заменить эти дополнительные эксперименты информацией из термического уравнения состояния.
Основное уравнение термодинамики получается в независимых переменных энтропии и объема. Для удобства работы используют преобразование Лежандра, которое позволяет перевести основное уравнение к другим независимым переменным и на этом пути получаются новые функции состояния — энтальпия (H), энергия Гельмгольца (A) и энергия Гиббса (G). Эти преобразования не требуют новых экспериментальных данных, но их использование существенно облегчает практическое использование уравнений классической термодинамики. Этот аспект будет рассмотрен в разделе ‘Преобразование Лежандра и новые функции состояния‘.
Наконец в разделе ‘Термодинамические таблицы‘ мы рассмотрим справочник ‘Термодинамические свойства индивидуальных веществ‘. Данные из этого справочника будут в дальнейшем использованы в главе ‘Адиабатическая температура пламени’; таким образом, настоящая глава уже имеет определенное отношение к горению свечи.
Калориметр и функции состояния
В предыдущей главе был рассмотрен калориметр. В этом разделе свяжем измерение количества теплоты в калориметре с функциями состояния. Перепишем первый закон в следующем виде:
dQ = dU + pdV
При постоянном объеме не происходит работы расширения и измеряемая теплота при постоянном объеме (Qv) равна изменению внутренней энергии:
dQv = dU => Qv = ΔU
Из измерений теплоты при постоянном объеме определяется теплоемкость при постоянном объеме:
Cv = (∂Q/∂T)v = (∂U/∂T)v
Эксперименты в калориметрии обычно проводятся при постоянном давлении, поэтому требуется уравнение для количества теплоты, измеренной при постоянном давлении (Qp). В этом случае удобно использовать ввести новую термодинамическую функцию энтальпию: H = U + pV. Ниже мы рассмотрим это уравнение как пример преобразования Лежандра, которое позволяет провести замену переменных в основном уравнении термодинамики. В этом разделе просто рассмотрим процесс измерения количества теплоты при постоянном давлении:
dQp = dU + pdV = d(U + pV) => Qp = ΔH
Таким образом, измерение количества теплоты при постоянном давлении дает изменение функции состояния энтальпии. Это уравнение также показывает, что энтальпия отличается от внутренней энергии работой расширения, но важно помнить, что сказанное относится только к процессам при постоянном давлении.
В любом случае энтальпия оказывается функцией состояния, которую удобно использовать при обработке данных калориметрических экспериментов при измерении теплоемкости при постоянном давлении:
Cp = (∂Q/∂T)p = (∂H/∂T)p
В принципе возможно использовать результаты этих экспериментов для расчета изменения внутренней энергии, но это потребовало бы использование термического уравнения состояния. Использование энтальпии позволяет отделить обработку результатов калориметрии при постоянном давлении от экспериментов по изучению термического уравнения состояния. Более того, многие расчеты проводятся при использовании независимых переменных давление и температура и для них удобнее использовать энтальпию. Так, в таблице термодинамических свойств приводится именно энтальпия, а не внутренняя энергия.
Ледяной калориметр использовался в том числе для определения теплоты, выделяющейся при протекании химических реакций; в первую очередь реакций сгорания. В идеальной тепловой машине Карно используются идеальные источники теплоты, в реальном мире используется энергия химических реакции. Одним из первых исследователей теплоты сгорания веществ в первой половине 19-ого века был Герман Гесс, работавший в Санкт-Петербургской академии наук. Он сформулировал закон Гесса:
‘Когда образуется какое-либо химическое соединение, то при этом всегда выделяется одно и то же количество тепла независимо от того, происходит ли образование этого соединения непосредственно или же косвенным путем и в несколько приемов.’
В настоящее время следует говорить об энтальпиях реакций, причем под энтальпией реакции понимается разность энтальпий продуктов и реагентов, когда энтальпия всех веществ берется при одинаковой температуре и давлении. Например, для реакции сгорания угля:
C(уголь) + O2 = CO2
∆rH = Hm(CO2, T, P) — Hm(C, уголь, T, P) — Hm(O2, T, P)
Термодинамические функции зависят от массы вещества (экстенсивные величины). Обычно в таблицах приводят значения для одного моля вещества, что подчеркивается подстрочным индексом m (мольная или молярная энтальпия).
В термодинамике можно определить только изменение энтальпии (внутренней энергии), поэтому для получения численных значений вводятся мольные энтальпии образования веществ, то есть, энтальпии реакции образования одного моля вещества из простых веществ в стандартном состоянии (∆fHm). Именно они приводятся в справочнике и далее используются при расчете энтальпий реакций.
Основное уравнение термодинамики
При подстановке теплоты из второго закона термодинамики в первый закон получается объединенное уравнение первого и второго закона, которое называется основным уравнением термодинамики. В силу наличия неравенства во втором законе возникают два варианта, основное уравнение:
dU = TdS — pdV
и основное неравенство:
dU < TexdS — pexdV
Чрезвычайно важно не путать одно с другим. В неравенстве используются температура и давление, задаваемые внешними условиями. Тем самым неравенство включает в том числе состояние вещества с градиентами температуры и давления. Неравенства задает критерий самопроизвольного процесса при заданных внешних условиях и тем самым позволяет позволяет вывести критерий равновесия, когда самопроизвольный процесс завершается. Мы рассмотрим основное неравенство и примеры его использования для определения равновесия в следующей главе.
В это главе мы рассмотрим основное равенство, запись которого подразумевает, что речь идет о состоянии вещества с однородной температурой и давлением; вид уравнения подчеркивает, что градиенты температуры и давления исключены из рассмотрения. Интегралы с использованием основного уравнения соответствуют равновесным процессам, однако результаты вычислений изменения функций состояния, полученные таким путем, будут такими же для всех процессов, включая неравновесные.
Простой пример — если мы знаем величину двух объемов в двух состояниях, то изменением объема будет разница этих величин, независимо от того, каким образом произошл процесс. Та же логика применяется для всех термодинамических функций состояния — внутренней энергии, энтропии, энтальпии, энергии Гельмгольца и энергии Гиббса; в этом смысл понятия функция состояния. Правда, приведенное основное уравнение относится к чистому веществу, в котором не проходят химические и фазовые реакции — предмету рассмотрения в этой части книги. Рассмотрение растворов требует расширение основного уравнения путем использования химических потенциалов.
После достижения вывода о том, что теплота не является функцией состояния, термин калорическое уравнение состояния стали относить к выражению внутренней энергии U(T, V) как функции температуры (T) и объема (V). Формально дифференциал внутренней энергии в этих переменных записывается при использовании двух производных:
Первая производная есть теплоемкость при постоянном объеме (связь с калориметрией), а для определения зависимости внутренней энергии от объема при постоянной температуре требуются специальные усилия. В истории физики 19-ого века опыты Гей-Люссака и Джоуля с газами позволили заключить, что для газов эта производная равна нулю. Правда, потом при повышении точности измерений оказалось, что вывод справедлив лишь для уравнения состояния идеального газа, а для реальных газов дело обстоит более сложным образом (опыты Джоуля-Томсона). Я не буду рассматривать эту историю, чтобы не перегружать изложение, для желающих ее можно найти в отдельной заметке (см. раздел ‘Информация‘ в конце главы).
Теперь рассмотрим энтропию как функцию состояния S(T, V). Формально она приводит к появлению двух новых производных:
Однако подстановка этого уравнения в основное уравнение термодинамики dU = TdS — pdV дает связь этих производных с производными внутренней энергии по температуре и объему:
В классической термодинамике также доказывается соотношение Максвелла, которое выражает производную энтропии по объему через термическое уравнение состояния (см. ниже энергию Гельмгольца для вывода):
Все вместе приводит к следующим выражениям для внутренней энергии U(T, V) и энтропии S(T, V):
Таким образом, для определения внутренней энергии и энтропии чистого вещества достаточно данных по теплоемкости при постоянном объеме и термического уравнения состояния. Эксперименты в калориметрии и изучение термического уравнения состояния (относительный коэффициент давления) ведут одновременно к функциям внутренней энергии и энтропии.
Несколько слов про понимание энтропии. Два уравнения выше показывают, что связь физических величин внутренней энергии и энтропии с проводимыми экспериментами по изучению термодинамических свойств аналогична — одни и те же эксперименты позволяют рассчитать обе физические величины. Конечно, эти уравнения нельзя рассматривать как определения внутренней энергии и энтропии. Определениями являются первый и второй закон соответственно, а эти уравнения являются следствиями, которые однако дают прямую связь с экспериментами. Следует отметить, что непосредственное использование первого и второго закона для расчета внутренней энергии и энтропии невозможно.
В этом контексте следует пока задуматься, можете ли вы уже дать ответ на вопрос ‘Что такое теплоемкость при постоянном объеме?’. Это позволит лучше понять ваши ожидания от ответа на вопрос ‘Что такое энтропия?’, к которому я вернусь в последней главе этой части.
Преобразование Лежандра и новые функции состояния
В основном уравнении термодинамики в качестве независимых переменных выступают энтропия и объем, а внутренняя энергия, температура и давления являются функциями: U(S, V), T(S, V), p(S, V). Следует также отметить, что температура является производной от внутренней энергии по энтропии: T = (∂U/∂S)V; это уравнение используется в обобщенной неравновесной термодинамике и в статистической механике.
В предыдущем разделе было проведено преобразование независимых переменных (S, V) к (T, V) без изменения основного уравнения. В то же время удобно провести замену переменных непосредственно в основном уравнении, поскольку это дает удобный путь решения практических задач. Преобразования Лежандра позволяют достичь этой цели. Так, введение энтальпии (H = U + pV) является преобразованием Лежандра, которое меняет местами давление и объем — давление становится независимым переменным, а объем производной энтальпии:
dH = TdS + Vdp
Энергия Гельмгольца (A = U − TS, старое обозначение энергии Гельмгольца: F) меняет местами температуру и энтропии, а энергия Гиббса (G = U + pV − TS = H − TS) является двойным преобразованием Лежандра, которое меняет местами обе пары переменных:
dA = −SdT − pdV
dG = −SdT + Vdp
Кстати, соотношение Максвелла в предыдущем разделе получается из выражения для энергии Гельмгольца как следствие равенства смешанных производных функции A(T, V). Уравнения выше представляют собой формальные математические определения новых функций состояния, связанных с заменой переменных. Эти математические операции ничего не добавляют к первому и второму закону термодинамики. По существу внутренняя энергия U(S, V), энтальпия H(S, p), энергия Гельмгольца A(T, V) и энергия Гиббса G(T, p) являются эквивалентными функциями состояния, поскольку знание одной из них позволяет получить остальные в ходе необходимых математических преобразований.
Энергия Гиббса находит широкое применение в практических расчетах, поскольку использование независимых переменных температура и давление соответствует условию проведения многих экспериментов, когда температура и давления задаются как внешние условия. Энергия Гельмгольца с другой стороны активно используется в равновесной статистической механике, она непосредственно связана со статистической суммой, которая в свою очередь используется для вычисления термодинамических свойств из молекулярных свойств.
Введение новых термодинамических функций в классической термодинамике при использовании выражения ‘для удобства’ вызывает определенный когнитивный диссонанс. С другой стороны, это обстоятельство позволяет еще раз обсудить отношения математики и мира. Например, возникает вопрос, существует ли энтальпия, энергия Гельмгольца и энергия Гиббса. На примере энтальпии ответ будет такой. Если у вещества есть функции состояния внутренняя энергия, давление и объем, то у него также есть свойство, которое выражается как энтальпия H = U + pV. В этом контексте выражение ‘для удобства’ связано с существованием в математике возможности эквивалентного преобразования исходных выражений. Это, конечно, поднимает непростые вопросы для метафизиков, которые озабочены устройством мира ‘на самом деле’ — существует ли внутренняя энергия, существует ли энтальпия, энергия Гельмгольца или энергия Гиббса. Но все это не вызывает проблем при решении практических задач.
Термодинамические таблицы
Справочник ‘Термодинамические свойства индивидуальных веществ‘ явился продуктом холодной войны, что наглядно подчеркивает название аналогичного американского справочника: Joint Army-Navy-Air Force Thermochemical Tables (JANAF Thermochemical Tables). В настоящее время термодинамические таблицы обоих справочников можно найти онлайн:
NIST-JANAF Thermochemical Tables
Термодинамические свойства индивидуальных веществ
Термодинамические таблицы организуют результаты огромного количества экспериментальных измерений в удобном виде для расчета энергии Гиббса химических реакций с целью последующего расчета равновесного состава. В настоящее время таблицы в такой форме устарели, поскольку вся процедура автоматизирована в программном обеспечении, в котором графический интерфейс позволяет организовать поиск в базе данных необходимых энергий Гиббса и дальнейшее проведение дальнейшего расчета равновесного состава с использованием необходимых численных алгоритмов.
Таблицы отталкиваются от химической идентификации чистых веществ; каждому веществу посвящена своя таблица, в которой термодинамические свойства табулированы как функция температуры при стандартном давлении. Отмечу, что для понимания выбранного стандартного состояния газов, в особенности малостабильных соединений и ионов, требуется знание химической термодинамики, поскольку в данном случае приведенные численные значения относятся к сильно идеализированному состоянию.
Рассмотрим фрагмент таблицы с термодинамическими свойствами кислорода:
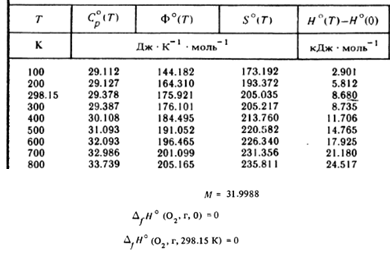
Приведены мольные значения; молярная масса приведена отдельно. Также отдельно приведены энтальпии образования при двух температурах, при 0 К и 25ºС (298.15 К). Надстрочный индекс º показывает, что термодинамические свойства относятся к стандартному давлению (на момент публикации справочника в 1978 году — 1 атм, в настоящее время 1 бар). При использовании термического уравнения состояние данные можно пересчитать к другому давлению.
В колонке с энтальпией приведена разность энтальпии при текущей температуре по отношению к энтальпии при 0 К. Однако в колонке с энтропией приведена абсолютная энтропия. Это связано с тем, что согласно третьему закону термодинамики энтропия вещества при 0 К равна нулю. Колонка с Φ облегчает расчет стандартной энергии Гиббса химической реакции, когда энтальпия реакции при 0 К рассчитывается из данных энтальпий образования при этой температуре:
∆rGº(T) = ∆rH(0 K) + ∆r[H(T) − H(0 K)] − T∆rS = ∆rH(0 K) − T∆rΦ
В компьютером представлении базы данных хранится только полином энергии Гиббса, поскольку все остальные термодинамические свойства находятся как производные этого полинома. Еще раз подчеркну математическую эквивалентность представления термодинамических свойств вещества, например, в виде функций U(S, V) и G(T, p). В любом случае производные дают все остальные термодинамические свойства; эти функции в данных независимых переменных называются поэтому характеристическими.
Разница состоит в независимых переменных, поскольку обычно при решении задач в химической термодинамики требуются термодинамические свойства при заданных температуре и давлении. В случае энергии Гиббса вычисления следуют непосредственно, а в случае внутренней энергии вначале требуется решить внутреннюю математическую задачу для нахождения необходимых значений независимых переменных, которые соответствуют заданным температуре и давлению. Таким образом, использование энергии Гиббса на практике связано с выбором удобных переменных для решения практических задач.
В главе ‘Адиабатическая температура пламени‘ будут даны два примера использования термодинамических таблиц. Здесь же только скажу, что появление обоих справочников было связана с задачами запуска ракет, когда похожие расчеты позволяли оценить реактивную тягу.
Далее: Глава 4. Неравенство Клаузиуса как критерий равновесия
Информация
Калорическое уравнение состояния: опыты Гей-Люссака и Джоуля-Томсона: История калорического уравнения состояния. Зависимость внутренней энергии от объема и энтальпии от давления при постоянной температуре. Введение энтропии позволяет вычислить эти производные из уравнения состояния.
Энтальпия и энергия Гиббса: математика и физика: Энтальпия и энергия Гиббса в классической термодинамике как пример формальных математических преобразований для получения более удобных выражений. Логика и практика их использования в термодинамике.
Термодинамические свойства индивидуальных веществ. Справочное издание в четырех томах, третье издание, 1978 — 1982.