Это старый вариант. Последний вариант вошел в обзор: Обратимые процессы в классической термодинамике
___
В термодинамике большую роль играет отличие между обратимыми и необратимыми процессами. Оно появляется при рассмотрения цикла Карно из утверждения, что только использование обратимых процессов позволяет достичь максимального коэффициента полезного действия (к. п. д.) в цикле Карно. Протекание необратимых процессов в тепловом двигателе приводит к тому, что теоретический максимальный к. п. д. в реальности не достигается.
Цикл Карно включает в себя обратимый изотермический процесс превращения теплоты в работу. Его возможность обеспечивается тем, что предполагается бесконечно малая разность температур между источником теплоты и рабочим телом. Я всегда был убежден, что это единственная возможность обратимого процесса с участием теплоты. Можно было дополнительно представить теплообмен между двумя резервуарами энергии, разница температур которых была бы бесконечно малой, но в этом не видно большого смысла.
Как оказалось, я ошибался и с известными ухищрениями можно вполне представить себе процесс обратимого теплообмена между двумя телами с разными температурами. Это является следствием задачи 1 из книги В. А. Зорича ‘Математические аспекты классической термодинамики‘; ниже идет ее рассмотрение.
Рассмотрим два бруска одинаковой длины и сечения, изготовленных из материала, теплоемкость которого не зависит от температуры. Первый брусок находится при температуре 100ºС, а второй при 0ºС. При соприкосновении брусков теплота переходит от более горячего к более холодному и в конце концов температура обоих брусков будет 50ºС. Ниже расчет изменения энтропии в этом процессе — для простоты теплоемкость каждого бруска принята равной единице.
Энтропия в процессе теплообмена между брусками, как и следовало ожидать, увеличивается; процесс является необратимым. Из полученного состояния невозможно вернуть бруски в исходное состояние без использования энергии извне. Ниже этот случай будет называться стандартным теплообменом.
Хитрый Зорич однако предложил следующее. Представим себе, что каждый из брусков разделен пополам адиабатической перегородкой. Теперь будем проводить теплообмен путем продвижения одного из брусков вдоль другого. Ниже эта идея показана схематически вместе с получающимися температурами в ходе перемещения бруска.
Исходная позиция — бруски не касаются друг друга:
| 100ºС | 100ºС | ||
| 0ºС | 0ºС |
Теперь перемещаем брусок на половину длины:
| 100ºС | 50ºС | |
| 50ºС | 0ºС |
В силу адиабатических перегородок теплообмен идет только среди соприкасающихся частей брусков. Делаем следующий шаг:
| 75ºС | 25ºС |
| 75ºС | 25ºС |
Теперь сделаем последний шаг, ведь брусок можно еще раз передвинуть:
| 50ºС | 25ºС | |
| 75ºС | 50ºС |
Обратите внимание, что достижение термического равновесия по частям привело к тому, что средняя температура нижнего бруска стала больше средней температуры верхнего бруска. Второй закон термодинамики не нарушен, теплота все время переходила от более горячего с более холодному телу, но при этом удалось передать от горячего тела к холодному больше энергии, чем без перегородки. Расчет изменения энтропии в этом случае показывает, что энтропия возросла в таком процессе на меньшую величину по сравнению со стандартным теплообменом: 0.021.
Важно обратить внимание, что передвижение бруска не требует дополнительной энергии, так как считается, что передвижение идет без трения и оно происходит на одной высоте; не требуется совершать работу против силы тяжести. В классической термодинамике подобные передвижения тела не редкость при обсуждении тех или иных проблем.
Следующий шаг, который предлагает Зорич — это увеличение числа разбиений и исследование предела, когда число разбиений стремится к бесконечности. Выводы в аналитическом виде не являются моим коньком, поэтому я просто написал небольшую программку — reversible_heat_exchange.py — которая рассчитывает конечную температуры в обоих стержнях при заданном числе разбиений. Ниже я приведу только один график (программка делает больше графиков и выводит больше информации).
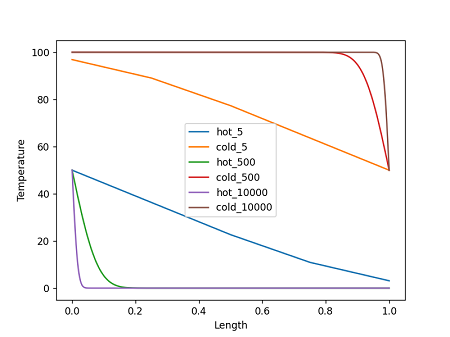
На графике показано температурное распределение в двух брусках после завершения процесса передвижения для трех разных разбиений брусков, на 5, 500 и 10000 частей. Температуры кусочков соединены прямыми линиями, что создает несколько неправильное представление в особенности в случае разбиения на 5 частей, там должны быть пять горизонтальных линий. Но мне было лень возиться, тем более что для больших чисел разбиений это не играет практически никакой роли.
Конечные температурные распределения бруска с исходной температурой 100ºС (hot) находятся внизу графика — в ходе такого процесса брусок охлаждается; при увеличении числа разбиений до 0ºС. В то же время брусок с исходной температурой 0ºС (cold) нагревается при увеличении числа разбиений до 100ºС. Температура самой левой точки бруска с исходной температурой 100ºС и самой правой точки бруска с исходной температурой 0ºС остается равной 50ºС. Однако области, прилежащие к этим точкам, при увеличении числа разбиений сужаются и при стремлении к бесконечности превратятся в дельта функции.
Программка делает расчет изменения энтропии как функции числа разбиений. Оно уменьшается и при устремлении числа разбиений к бесконечности стремится к нулю. Предложенный Зоричем процесс будет обратимым процессом передачи теплоты от одного бруска (100ºС) к другому (0ºС) при бесконечном числе разбиений! Если бы я не увидел это своими глазами, то никогда бы не поверил, что такое возможно. Суть происходящего связана с тем, что в качестве бесконечно малого рассматривается не разница температур, как в изотермическом процессе обратимого цикла Карно, а количество нагреваемого вещества. Очень красиво, снимаю шляпу перед мудростью математиков.
Возникает вопрос, как можно было бы осуществить нечто подобное. Ответ связан с использованием анизотропных материалов. Бесконечное число разбиений соответствует материалу с анизотропной теплопроводностью, когда теплопроводность по направлению между брусками бесконечно больше теплопроводности в двух других направлениях. Конечно, это идеализация, но обратимый цикл Карно сам по себе также является идеализацией.
Итак, представим себе два бруска а такой анизотропной теплопроводностью. Исходная температура одного бруска 100ºС, а другого 0ºС. Теперь бесконечно медленно проводим один брусок мимо другого. Бац, бруски поменялись температурами. Можно теперь двигать бруски в обратном направлении и опять произойдет обмен температурами. При этом второй закон нисколько не нарушается, теплота все время переходит от более горячего к более холодному телу. Таким образом, обратимый процесс теплообмена между двумя телами с разными температурами вполне возможен. Я в восхищении.
Содержание: Термодинамика
Информация
Владимир Антонович Зорич, Математические аспекты классической термодинамики, 2019.
Обсуждение
https://evgeniirudnyi.livejournal.com/352706.html
30.03.24 Число и тепло
Эпиграф из книги:
‘Что мы знаем о числе?
Ничего, но знают все.
Что мы знаем о тепле?
То же, что и о числе.’
