Замерзание переохлажденной воды

Ранее: Законы термодинамики. Простейший пример тепловой смерти

Продолжу рассмотрение возрастания энтропии в изолированной системе на примере переохлажденной воды при -2°С (271.15 К). Напомню, что если проводить медленное охлаждение воды в специальном сосуде, где отсутствуют центры кристаллизации, то можно переохладить воду ниже температуры замерзания. Переохлажденная вода находится в метастабильном состоянии и она будет самопроизвольно переходить в лед либо при внесении центров кристаллизации, либо в результате флуктуаций; хотя в последнем случае возможно придется несколько подождать.

Этот пример хорош тем, что энтропия переохлажденной воды больше энтропии льда, что не помешает началу процесса превращения переохлажденной воды в лед. Правда, в изолированной системе все закончится гетерогенным равновесием из льда и воды при температуре фазового равновесия. Тем не менее, это даст возможность для любителей метафоры порядка и беспорядка сравнить хаос в переохлажденной воде с таковым при достижения гетерогенного состояния из льда и воды.

Обычно фазовые равновесия обсуждаются для закрытых систем при постоянном давлении и температуры. В этих координатах строится фазовая диаграмма, на которой видны условия существования фаз: льда, воды, паров воды и фазовых равновесий между ними. При постоянном давлении и температуре условием самопроизвольного протекания процессов и критерием равновесия является энергия Гиббса, которая стремится к минимуму.

Рассмотрим фазовую реакцию плавления льда:

H₂0(лед) = H₂0(вода)

Протекание реакции в ту или иную сторону при постоянных давлении и температуре определяется энергией Гиббса реакции, которая в свою очередь связана с энтальпией и энтропией реакции:

ΔG = ΔH — TΔS

Символ Δ означает разницу мольных энергий Гиббса воды и льда при заданных температуре и давлении (в нашем случае атмосферном давлении):

ΔG = G(T, p, 1 моль воды) — G(T, p, 1 моль льда)

Для упрощения выкладок будем использовать приближение независимости теплоемкостей от температуры; более того, примем, что теплоемкость воды равна теплоемкости льда. Таким образом: ΔC_p = 0. Мольные теплоемкости воды и льда на самом деле несколько отличаются [75 Дж/(моль К) и 38 Дж/(моль К) соответственно]. Лучшим приближением было бы ΔC_p = const, но это несколько усложнит выкладки, поэтому будет использоваться среднее значение теплоемкости 56.5 Дж/(моль К) как для воды, так и для льда. В этом приближении энтальпия и энтропия реакции не зависит от температуры: ΔH = const и ΔS = const.

Рассмотрение фазовой реакции превращения льда в воду при постоянном давлении и температуре сводится к знаку энергии Гиббса. Для анализа удобно вначале выразить энтропию плавления через энтальпию плавления:

Δ S = \frac{Δ H}{T_{e q}}

Уравнение выше получается из равенства ΔG = 0 при равновесной температуре плавления (T_eq). Важно отметить, что плавление льда требует энергии и энтальпия плавления положительна (6010 Дж/моль). Это в свою очередь приводит к положительной энтропии плавления льда — энтропия воды больше энтропии льда.

Энергию Гиббса фазовой реакции теперь можно выразить только через энтальпию плавления и текущую температуру:

Δ G = Δ H (1 — \frac{T}{T_{e q}})

В таком виде ниже представлен анализ возможных состояний; напомню, что при постоянном давлении и температуре критерием равновесия является минимум энергии Гиббса, при этом фазовая реакция идет до конца в случае в случае отличия энергии Гиббса от нуля:

\begin{matrix} T = T_{e q} & Δ G = 0 & равновесие \\ T > T_{e q} & Δ G < 0 & устойчива вода \\ T < T_{e q} & Δ G > 0 & устойчив лед \end{matrix}

Преимущества рассмотрения химических и фазовых реакций при постоянном давлении и температуре связано с процедурой осуществления такого состояния: температура задается термостатом, давление — атмосферой. При этом теплообмен с окружением позволяет не думать о влиянии выделяющейся или требующейся энергии для протекания реакции; термостат сохраняет температуру постоянной.

В изолированной системе выделяющаяся энергия идет на нагрев компонентов системы и таким образом температура системы зависит от степени протекания реакции. Выкладки несколько усложняются, но в рамках сделанного приближения о равенстве теплоемкостей воды и льда уравнения остаются еще сравнительно простыми. Правда, в случае изолированной системы потребуется еще одно приближение о равенстве мольных объемов (плотностей) воды и льда: ΔV = 0. В изолированной системе внутренняя энергия и объем постоянны. Без приближения выше протекание фазовой реакции будет вести к изменению давления, которое, строго говоря, влияет на фазовое равновесие. Это в свою очередь усложняет выкладки.

С другой стороны, можно сказать, что рассмотрение ниже будет проведено для теплоизолированной системы с постоянным давлением. В этом случае энтропия также является критерием равновесия:

{(d S)}_{H, p} \geq 0

В случае приближения о равенстве мольных объемов это совпадет с рассмотрением изолированной системы:

{(d S)}_{U, V} \geq 0

Для удобства перепишем фазовую реакцию в обратном направлении и введем химическую переменную x:

\begin{matrix} H_{2} 0 (вода) & = & H_{2} 0 (лед) \\ n_{0} — x & x \end{matrix}

В начальном состоянии есть n₀ молей переохлажденной воды, x показывает уменьшение числа молей воды, а также число молей образовавшегося льда. Отмечу, что энтропия и энтальпия замерзания воды меняют знак по сравнению с таковыми величинами при плавлении льда. Ниже по-прежнему будут рассматриваться энтальпия и энтропия плавления льда.

Начнем с баланса энергии, она остается постоянной — энтальпия реакции идет на нагревание компонентов (воды и льда). В данном случае только следует отметить, что формально энтальпия замерзания воды отрицательна, поскольку в экзотермической реакции считается, что энергия отдается окружению. В нашем случае энергия остается в системе и поэтому следует использовать положительное значение энтальпии плавления — температура компонентов должна увеличиться.

Еще раз отмечу, что приближение о равенстве теплоемкостей воды и льда делает это уравнение достаточно простым, что в свою очередь дает простое выражение для температуры компонентов как функции химической переменной (T₀ — начальная температура переохлажденной воды):

Q = x Δ H = {C_{p} (n_{0} — x) + C_{p} x} (T — T_{0}) = n_{0} C_{p} (T — T_{0})

T = \frac{x Δ H}{n_{0} C_{p}} + T_{0}

Следующий шаг — выражение для энтропии системы как функции химической переменной. Ниже индекс 1 относится к воде, а индекс 2 ко льду. Также приближение о равенстве теплоемкостей воды и льда делает это выражение сравнительно простым:

S = (n_{0} — x) S_{1} + x S_{2}

S = (n_{0} — x) [S_{1, 0} (T_{0}) + C_{p} l n (\frac{T}{T_{0}})] + x [S_{2, 0} (T_{0}) + C_{p} l n (\frac{T}{T_{0}})]

S = n_{0} S_{1, 0} (T_{0}) + n_{0} C_{p} l n (\frac{T}{T_{0}}) — x Δ S

Последнее уравнение получено после перегруппировки слагаемых. В нем можно выделить начальную энтропию переохлажденной воды, изменение энтропии воды и льда при нагревании и изменение энтропии реакции. Использовано положительная энтропия плавления льда, поэтому перед последним слагаемым появился минус. Нагревание компонентов увеличивает энтропию, протекание реакции ее уменьшает.

Теперь подставим выражение для температуры как функции химической переменной и также выразим энтропию плавления через энтальпию; получится заключительное выражение для изменения энтропии как функции химической переменной. Поскольку энтропия переохлажденной воды в начальном состоянии является константой, она перенесена в левую часть уравнения:

S — n_{0} S_{1, 0} (T_{0}) = n_{0} C_{p} l n (\frac{x Δ H}{n_{0} C_{p} T_{0}} + 1) — x \frac{Δ H}{T_{e q}}

График правой части (n₀ = 1) приведен ниже. Левая ось ординат показывает изменение энтропии, правая — температуру системы:

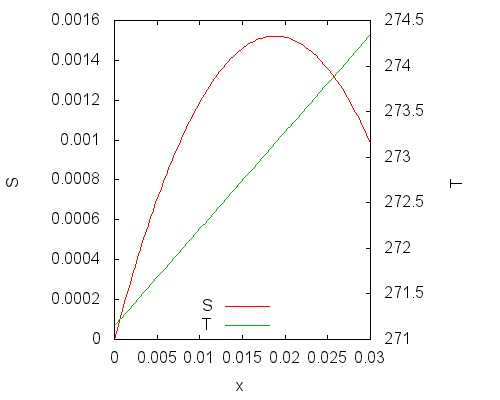
/ru/wp-content/uploads/2023/12/ice_water.png

Видно, что замерзание переохлажденной воды по мере протекания реакции (увеличение химической переменной x) вызывает рост температуры компонентов. До определенного значения рост температуры компонентов перевешивает уменьшение энтропии в ходе реакции и энтропия системы возрастает. После определенного значения, которое соответствует равновесию, энтропия начинает убывать. Это связано с тем, что получается перегретый лед.

Максимум энтропии соответствует равновесной температуре плавления льда. На графике этот факт не так заметен, но это можно увидеть при взятии производной от последнего уравнения — после ряда операций по упрощению получается следующее несложное уравнение для химической переменной при равновесии:

d S / d x = 0 ⟹ x = n_{0} C_{p} (T_{e q} — T_{0}) / Δ H

Можно проверить, что именно это значение химической переменной дает температуру компонентов, равную T_eq.

Итак, в рамках ряда упрощений получается сравнительно несложное описание процесса замерзания переохлажденной воды в теплоизолированной системе. Оно наглядно показывает происходящее: уменьшение энтропии в ходе образования льда из переохлажденной воды компенсируется нагревом смеси. В результате получается гетерогенная система из льда и воды при равновесной температуре фазового перехода. Этой системе соответствует максимум энтропии, поскольку дальнейшее протекание реакции привело бы к образованию перегретого льда.

Далее: Глобальное и локальное тепловое равновесие в классической термодинамике

Приложение

Сценарий Gnuplot для построения графика:

set terminal png enhanced size 500,400
set output 'fig1.png'
set xlabel 'x'
set ylabel 'S'
set y2label 'T'
set y2tics
set ytics nomirror
set key center bottom
plot [x=0:0.03] 56.5*log(x*6010/(56.5*271.15)+1)-x*6010/273.15 title 'S', 271.15+x*6010/56.5 axis x1y2 title 'T'

Обсуждение

https://evgeniirudnyi.livejournal.com/345363.html