Парадокс Гиббса в классической термодинамике

Ранее: Замерзание переохлажденной воды

Посмотрел про историю парадокса Гиббса: книгу С. Д. Хайтуна ‘История парадокса Гиббса‘ и обзор Оливье Дарриголя ‘Парадокс Гиббса: ранняя история и пути решения‘. Меня удивило, что как в книге Хайтуна, так и обзоре Дарриголя выражались сомнения в возможности разрешения парадокса Гиббса в рамках классической термодинамики. В конце 19-ого — начала 20-ого века понятие энтропии в химии приживалось с трудом и можно понять вопросы и колебания, возникающие в те времена у ученых в связи с энтропией смешения. С другой стороны, химическая термодинамика является сложившейся наукой и с моей точки зрения ничего парадоксального в парадоксе Гиббса в классической термодинамике не осталось.

Ниже буду отталкиваться от книги Хайтуна, где парадокс сформулирован в виде трех вопросов, которые в целом соответствуют описанию ситуации в труде Гиббса 1876 года:

• ‘Что такое смесь разных идеальных газов в отличие от «смеси» одинаковых?
• Как обеспечить предельный переход от смешения разных газов к «смешению» одинаковых?
• Почему величина скачка не зависит от природы смешиваемых газов, от степени их подобия?’

Для понимания сказанного придется выписать ряд уравнений; я ограничусь рассмотрением энергии Гиббса двухкомпонентного раствора A-B. Обычно парадокс рассматривается для энтропии смешения, но поскольку энергия Гиббса G тесно связана с энтропией S (G = H — TS, T является абсолютной температурой и H энтальпией), то все сказанное выше без изменения относится к энергии Гиббса. Меняется лишь знак: энтропия смешения положительна, а энергия Гиббса смешения отрицательная.

Отмечу, что статья Дарриголя заканчивается разделом, посвященном связи теории и эксперимента, в котором Дарриголь правильно отмечает, что теория представляет собой символическую запись в математической форме и ее применение требует интерпретации. Будем следовать этой рекомендации. Заранее скажу, что я старался упростить рассмотрение насколько это возможно, тем не менее, введение в тему не удалось свести к двух предложениям; поэтому без определенных усилий не обойтись.

Представим себе две системы, находящиеся в равновесии с окружением с температурой T и давлением p, разделенные перегородкой. При удалении перегородки получается новая система. Начнем рассмотрения этого процесса с отличия интенсивных переменных от экстенсивных. Так, температура и давление не изменятся, они относятся к интенсивным переменным. В то же время энергия Гиббса зависит от изменения количества вещества, она вместе с энтальпией и энтропией относится к экстенсивным переменным.

В химической термодинамике количество вещества измеряется в числах молей n; в двухкомпонентной системе задаются числа молей n₁ и n₂, соответствующие числу молей первого и второго компонента. Все экстенсивные свойства в химической термодинамике относятся к однородным функциям первого порядка, что выражается следующим уравнением

$$G\left(T,p,k{n}_1,k{n}_2\right)=kG\left(T,p,n_1,n_2\right)$$

Увеличение всех чисел молей в k раз приводит к увеличению значения функции в k раз. Другими словами, если взять одну и ту же систему два раза при одинаковых значениях интенсивных переменных, то суммарная энергия Гиббса складывается из энергий Гиббса составляющих систем.

В выражении выше неявно присутствует еще одна интенсивная переменная — состав системы; отношение n₁ к n₂, оно должно оставаться постоянным. Введем состав в явном виде, для чего заменим n₁ и n₂ на суммарное число молей n = n₁ + n₂ и мольные доли: x₁ = n₁/n и x₂ = n₂/n. Сумма мольных долей равна единице и таким образом из двух независимых переменных n₁ и n₂ остаются две независимые переменные, в качестве которых будут использованы n и x₂. Обратите внимание, что мольная доля является интенсивной переменной. Для упрощения уравнений ниже я также буду использовать x₁ вместо (1 — x₂).

При рассмотрении энергии Гиббса смешения удобно записать энергию Гиббса системы через химические потенциалы компонентов. Уравнение ниже является математическим следствием принадлежности энергии Гиббса системы к однородным функциями первого порядка, то есть, уравнение ниже является точным

$$G=n_1{\mu }_1+n_2{\mu }_2$$

Ниже я перепишу это уравнение с введением в рассмотрение состава системы и суммарного числа молей в явном виде

$$G\left(T,p,x_2,n\right)=n\left[x_1{\mu }_1\left(T,p,x_2\right)+x_2{\mu }_2\left(T,p,x_2\right)\right]$$

Это уравнение показывает зависимость энергии Гиббса от суммарного числа молей бинарной системы, а также в нем отмечается факт, что химический потенциал как производная энергии Гиббса является интенсивной функцией; он не зависит от суммарного числа молей — химический потенциал является функцией только температуры, давления и состава.

Энергия Гиббса смешения по определению вводится как разница между энергией Гиббса получившейся системы и суммой энергий Гиббса исходных подсистем. В случае смешения n₁ молей компонента А и n₂ компонента В из энергии Гиббса получившегося раствора надо вычесть энергии Гиббса чистых компонентов, которые можно выразить через химические потенциалы чистых компонентов (символ ^o в выражении для химического потенциала)

$${\Delta }_{mix}G\left(T,p,x_2,n\right)=G\left(T,p,x_2,n\right)—n\left[x_1{\mu }_1^o\left(T,p\right)+x_2{\mu }_2^o\left(T,p\right)\right]$$

Вышесказанное являлось рассмотрением понятий химической термодинамики без введения приближений. Для расчетов по приведенному уравнению необходимо иметь выражение для химического потенциала. При рассмотрении газов существует закон Дальтона: при смешении газов суммарное давление выражается как сумма парциальных давлений. При использовании закона Дальтона и в предположении, что каждый газ подчиняется уравнению состояния идеального газа, Гиббс получил выражение для химического потенциала одного компонента. Ниже оно записано в случае многокомпонентного раствора

$${\mu }_i\left(T,p,x_2,\dots ,x_N\right)={\mu }_i^o\left(T,p\right)+RTln{x}_i$$

В этом случае химический потенциал зависит только от мольной доли этого компонента, а влияние других компонентов раствора ограничено изменением мольной доли этого компонента. В химической термодинамике такой раствор получил название идеального и теперь можно перейти к конечному выражению для энергии Гиббса смешения идеального раствора А-В из компонентов А и В

$${\Delta }_{mix}^{ideal}G\left(T,p,x_2,n\right)=nRT\left(x_{1}ln{x}_1+x_{2}ln{x}_2\right)$$

При смешении полмоля А и полмоля В получается часто встречаемое выражение для энергии Гиббса смешения –RTln2 (энтропия смешения равна Rln2). Должно быть понятно, что выражение выше нельзя использовать в случае смешения полмоля В и полмоля В, поскольку в этом случае состав не меняется и записанное уравнение неприменимо. То есть, на уровне записанных выше уравнений парадоксов нет, парадокс возникает при переходе от уравнений в лабораторную практику.

Важно отметить, что Гиббс прекрасно понимал происходящее с математической точки зрения. Для понимания трех вопросов Гиббса в формулировке Хайтуна нам надо перенестись обратно на уровень экспериментальных знаний 1876 года. Из уравнений следовало следующее. Когда экспериментатор вынимает перегородку, разделяющие газы А и В, энергия Гиббса смешения и энтропия смешения меняется, при этом ее изменение не зависит от природы газов. В то же время, в аналогичном процессе с точки зрения экспериментатора вынимание перегородки, разделяющей часть В от другой части В приводит к нулевой энергии Гиббса смешения и энтропии смешения. При этом Гиббс вообразил существование непрерывного перехода от чуть-чуть отличающихся газов к одинаковому газу. В этом случае при минимальном изменении в газе наблюдался бы скачок энергии Гиббса смешения от –RTln2 к нулю.

Все осложнялось тем, что понятие энтропии находилось в становлении, а термин смешение вводил подозрение, что энтропия смешения каким-то образом связана с процессами диффузии при смешении. Диффузия отчетливо происходит в случае смешения А и В, но подобные молекулярные процессы происходят в случае смешения В и В. В этом случае важно отметить, что энтропия является функцией состояния и поэтому ее изменение связано исключительно с использованием конечных состояний. Способ достижения этих состояний не влияет на значение энтропии.

Также тогда не существовало экспериментальных методов для измерения энтропии или энергии Гиббса смешения. То есть, в те времена было сложно проверить правильность полученного теоретического значения. С другой стороны, экспериментальное изучение поведения газов и смесей газов с хорошей точностью также находилось на начальной стадии и поэтому уравнению состояния идеального газа и закону Дальтона придавалось значение фундаментальных законов. Все вместе взятое показывает, что обсуждение парадокса Гиббса (термин, введенный Пьером Дюгемом в 1892 году) в те времена было вполне полезным и оправданным делом.

Я же вернусь в настоящее время и рассмотрю вопросы, сформулированные Хайтуном, с точки зрения современных знаний. Начну с того, что изучение поведения реальных газов показало, что уравнение состояния идеального газа и закон Дальтона можно использовать только в пределе, когда общее давление стремится к нулю. В общем случае они не работают и требуется экспериментальное изучение термического уравнения состояния газов и их смесей — реальная энергия Гиббса смешения отличается от таковой в модели идеального раствора. Другими словами, говорить о независимости энергии Гиббса смешения от природы газа в настоящее время нельзя. Можно, конечно, говорить об одинаковом поведении энергии Гиббса смешения всех идеальных растворов, но вряд ли в этом будет большой смысл, поскольку переход от модели идеального раствора к практике показывает ограниченность применения этой модели.

Формализм выше требует идентификации компонентов при изучении растворов. На практике для этого используется химические и физико-химические методы. По ходу времени может оказаться, что рассматриваемый компонент раствора на самом деле сам является раствором компонентов, которые ранее не отличали друг от друга в силу отсутствия соответствующего метода анализа. Хороший пример связан с открытием изотопов — во времена Гиббса о них не знали, а в настоящее время изотопный состав поддается экспериментальному определению.

Вернемся к идеальному раствору А-В, для которого во времена Гиббса было показано, что энергия Гиббса смешения полмоля А и полмоля В равно ‑RTln2. Скажем, что за прошедшее время было установлено, что на самом деле компонент А является смесью изотопов А₁ и А₂, а компонент В является смесью изотопов В₁ и В₂. Как это повлияло на энергию Гиббса смешения? Правильный ответ — никак. Если взять четырехкомпонентный раствор А₁, А₂, В₁, В₂ и рассчитать энергию Гиббса смешения конечного раствора из полмоля раствора изотопов А₁ и А₂ и полмоля раствора изотопов В₁ и В₂ энергия Гиббса смешения останется равной –RTln2. Я не буду приводить выкладки, кто хочет может проверить сам. Важно только учесть, что соотношение изотопов не меняется в ходе образования раствора.

Рассмотрение изотопов в явном виде и введение энергии Гиббса смешения изотопов А₁ и А₂ потребуется при разделении изотопов. Это дает ответ на вопрос о разделении смеси разных газов от «смеси» одинаковых. Если состав раствора, образующего один компонент, остается постоянным во всех последующих операциях, можно рассматривать его как один независимый компонент. Введение дополнительных компонентов в этом случае не повлияет на результат, но только усложнит расчеты.

В статье Дарриголя при обсуждении решений парадокса Гиббса в классической термодинамики было сделано такое заявление: ‘нет единого мнения о том, как следует определять энтропию, даже на уровне макроскопической термодинамики’. Имелось в виду, что расчет изменения энтропии согласно второму закону возможен лишь при измерении количества теплоты в обратимом процессе (dS = dQ/T). В то же время процесс смешения является необратимым процессом и таким образом непосредственное измерение энтропии смешения невозможно.

В данном случае важно не забывать, что энтропия является функцией состояния. Поэтому для ее экспериментального определения вовсе не обязательно использовать выражение энтропии во втором законе. Современная практика изучения энтропии смешения следующая. В калориметрии изучается энтальпия смешения (для идеального раствора энтальпия смешения равна нулю), а далее тем или иным способом проводятся измерения химических потенциалов компонентов. Этих данных достаточно для определения энтропия смешения изучаемого раствора. В этом смысле Дарриголь неправ — в химической термодинамике нет расхождений по поводу того, как следует определять энтропию.

Еще одно замечание общего характера, поскольку некоторые горячие головы заявляют об субъективности энтропии и в том числе энтропии смешения. Согласно критерию устойчивости раствора энергия Гиббса смешения и энтропия смешения должна быть выпуклой. В противном случае раствор является неустойчивым и он распадается на два сосуществующих раствора с разными составами. Этот эффект носит название расслаивание и он наблюдается во многих растворах — далеко не все компоненты полностью растворяются в других компонентах. Эффект расслаивания также наблюдается в газовых смесях при больших давлениях.

Теперь рассмотрю вопрос предельного перехода. Еще раз, во времена Гиббса можно было над этим задуматься. В настоящее время согласно последним данным разведки непрерывный переход от одного индивидуального вещества к другому отсутствует, а протекание химических реакций в процессе смешения компонентов исключено по определению. Это обстоятельство дает один возможный современный ответ на вопрос Гиббса о предельном переходе. Другой вариант связан, например, с рассмотрением смешения полмоля В и полмоля раствора А-В. Изменение состава раствора А-В позволяет перейти от смешения А и В (мольная доля В в А-В равна нулю) к смешению В и В (мольная доля В в А-В равна единице) непрерывным путем путем изменения мольной доли В в растворе А-В от нуля до единицы.

В книге Хайтуна рассказана душераздирающая история о французском ученом Шамбадале, который пошел последним путем, но допустил ошибку в расчетах и него остался скачок в энтропии смешения. В отчаянии Шамбадаль представил доказательство, что энтропия смешения идеального раствора всегда равна нулю. Конечно, ошибку Шамбадаля быстро обнаружили, но самое парадоксальное, что Хайтун в любом случае посчитал, что парадокс Гиббса неразрешим в классической термодинамике.

Ниже мое рассмотрение, правда без вывода, для энергии Гиббса смешения полмоля В и полмоля раствора А-В. Формально ставится задача найти разность между энергией Гиббса получившегося раствора справа и исходных компонентов слева

$$G_B\left(T,p,n_B\right)+G_{AB}\left(T,p,x,n_{AB}\right)\Rightarrow G_{AB}\left(T,p,x_2,n\right)$$

n_B — это число молей исходного В, n_AB — число молей исходного раствора А-В, в котором под x понимается мольная доля В. С правой стороны n = n_B + n_AB означает получившееся число молей конечного раствора, а x₂ — мольную долю В в конечном растворе; она отличается от x в силу добавления В. Учет материального баланса дает следующие выражения для мольных долей А и В в конечном растворе; заключительное выражение справа дано при n_B = 0.5 моля и n_AB = 0.5 моля

$$x_1=\frac{\left(1—x\right)n_{AB}}{n}=0.5(1—x)$$ $$x_2=\frac{\left(1+x\right)n_{AB}}{n}=0.5(1+x)$$

Таким образом, при x = 0 (чистый А в исходном растворе А-В) получается смешение А с В, а при x = 1 (чистый B в исходном растворе А-В) получается смешение B с В. Значения между ними обеспечивают непрерывный переход от одному к другому. Выкладки приводят в следующему выражению энергии Гиббса смешения как функции от x (для удобства RT перенесено в левую часть)

$${\Delta }_{mix}^{ideal}G/\left(RT\right)=0.5\left(1+x\right)ln\left[0.5\left(1+x\right)\right]+0.5\left(1—x\right)ln0.5—0.5xlnx$$

График ниже отображает эту функцию. Ось Y слева показывает значение функции, а ось Y справа мольные доли x₁ и x₂ в получившемся растворе. По оси X отложена мольная доля x в исходном растворе А-В.

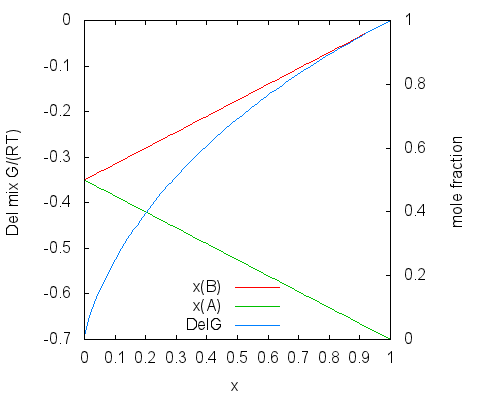
Функция при x = 0 равна –ln2 (требуемому значению при смешении чистых А и В), а при x = 1 равна нулю, как и следовало ожидать при смешении В с В. Промежуточные значения обеспечивают плавный переход от одного к другому.

Далее: Обратимый процесс теплообмена между двумя брусками с разными температурами

Информация

Хайтун Сергей Давыдович, История парадокса Гиббса. Изд. 3-е, 2010.

Darrigol, Olivier. The Gibbs paradox: Early history and solutions. Entropy 20, no. 6 (2018): 443.

Код для Gnuplot для построения графика:

set terminal png enhanced size 500,400
set output 'fig1.png'
set xlabel 'x'
set ylabel 'Del mix G/(RT)'
set y2label 'mole fraction'
set y2tics
set ytics nomirror
set key center bottom
plot [x=1e-5:1] 0.5*(1+x) axis x1y2 title 'x(B)', 0.5*(1-x) axis x1y2 title 'x(A)', 0.5*(1+x)*log(0.5*(1+x))+0.5*(1-x)*log(0.5)-0.5*x*log(x) title 'DelG' 
reset

Обсуждение

https://evgeniirudnyi.livejournal.com/360172.html