Ранее: Эволюция взглядов Людвига Больцмана на характер молекулярно-кинетической теории
Содержание: Термодинамика
Статистическое объяснение Людвига Больцмана о появлении стрелы времени в рамках обратимых законов механики остается популярным до настоящего времени. Уровень классической механики является недостаточным для рассмотрения атомов и молекул, но уравнения квантовой механики также симметричны во времени и переход на этот уровень не дает решения проблемы стрелы времени. Поэтому достаточно часто ограничиваются рассмотрением проблемы в рамках классической статистической механики в квазиклассическом приближении. В некоторой степени это обстоятельство поддерживает в ходу наглядную картину летающих бильярдных шаров.
Ниже рассмотрено использование этого подхода в книге Роджера Пенроуза ‘Мода, вера, фантазия и новая физика Вселенной‘, после чего будут обсуждены границы использования этого объяснения.
‘Что же в таком случае представляет собой эта «мера энтропии»? Грубо говоря, мы подсчитываем все возможные различные субмикроскопические состояния, которые могли бы образовать конкретное макроскопическое состояние, и их число N является мерой энтропии макроскопического состояния. Чем больше оказывается N, тем больше энтропия.’
‘В сущности, это и есть знаменитое определение энтропии, которое дал в 1872 году великий австрийский физик Людвиг Больцман.’
‘лучше всего вновь обратиться к формализму фазового пространства … фазовое пространство P некоторой физической системы концептуально представляет собой пространство, обычно содержащее огромное число измерений, и каждая точка такого пространства соответствует полному описанию субмикроскопического состояния (допустим, классической) физической системы, которую мы рассматриваем.’
‘Теперь, чтобы определить энтропию, нам потребуется собрать вместе — в единую область, именуемую регион крупнозернистого разбиения, — все те точки в P, в которых мы полагаем значения всех макроскопических параметров одинаковыми. Таким образом, все P будет разделено на такие крупнозернистые области. … Следовательно, фазовое пространство P будет делиться на такие регионы, и можно сказать, что объем V подобного региона позволяет оценить, сколько существует вариантов заполнения данного макроскопического состояния различными субмикроскопическими состояниями в границах данного региона крупнозернистого разбиения.’
‘Для того чтобы оценить, как это помогает понять второй закон, важно прочувствовать, сколь колоссально могут различаться по размеру различные области крупнозернистого разбиения, по меньшей мере в ситуациях, которые встречаются на практике. Логарифм в формуле Больцмана вкупе с чрезвычайной малостью k [константы Больцмана] в обыденных масштабах несколько маскирует всю беспредельность таких различий объема. Поэтому легко упустить тот факт, что крошечная разница в энтропии по факту соответствует просто огромной разнице объемов пространств с крупнозернистым разбиением. … Поскольку несравнимо более крупному объему соответствует обычно лишь чуть более высокая энтропия, мы уже примерно представляем себе, почему энтропия будет неудержимо возрастать с течением времени. Именно этого и следует ожидать согласно второму закону.’
Для иллюстрации вышесказанного приведу картику с сайта universe-review.ca — Thermodynamics:
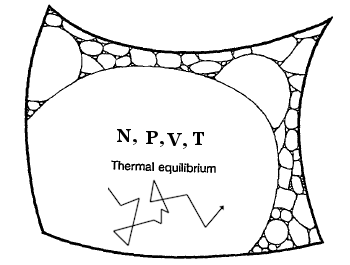
Изложение Пенроуза выше близко к выводам Больцмана в статье 1877 года; разница только в замене числа микросостояний объемом фазового пространства, содержащем эти микросостояния. Пенроуз однако знаком с историей обсуждения предложения Больцмана и поэтому он затем переходит к проблеме появления низкоэнтропийного состояния.
‘Асимметрия во времени возникает лишь потому, что сам вопрос, который мы задаем в отношении системы, по сути асимметричен, а именно: мы хотим выяснить вероятное поведение системы в будущем, исходя из ее актуального макроскопического состояния.’
‘Однако давайте посмотрим, что произойдет, если мы переформулируем вопрос, обратив время вспять. Допустим, имеется макроскопическое состояние со сравнительно низкой энтропией … Теперь давайте поинтересуемся не тем, что, скорее всего, произойдет с водой в будущем, а тем, в результате каких прошедших событий могла возникнуть такая ситуация. … повторив те же рассуждения, которые успешно описывали ход времени из прошлого в будущее, мы, вероятно, придем к выводу о том, что наша точка с гораздо большей вероятностью проникнет из значительно более обширного объема, чем из более мелкого, – то есть из состояния с более высокой энтропией, а не с более низкой.’
‘Разумеется, это прямо противоречит второму закону, поскольку мы, кажется, только что пришли к такому выводу: если бы мы отправились в прошлое, то энтропия вокруг неуклонно стала бы возрастать. Иными словами, анализируя любую ситуацию с достаточно низкой энтропией, мы бы с огромной вероятностью обнаружили, что ранее в природе действовал закон, обратный второму закону термодинамики!’
Это часть рассмотрения Пенроуза аналогична флуктуационной гипотезе Больцмана (см. Мозг Больцмана в равновесной Вселенной). Важно отметить, что в данном случае происходит переход к космологии — предполагается, что наблюдатель является частью рассматриваемой изолированной системы. Поскольку самое вероятное состояние такой системы равновесное, делается вывод, что маловероятное неравновесное состояние произошло из равновесного состояния.
Космологи убирают ветвь из второй части рассмотрения Пенроуза посредством ‘гипотезы о прошлом’ — предположении, что в момент большого взрыва энтропия была минимальной, что просто убирает вторую ветвь из рассмотрения. С другой стороны, есть последователи флуктуационной гипотезы Больцмана, когда стрела времени связывается с особенностями восприятия человека — человеческое время тождественно возрастанию энтропии. Для примера, ниже несколько цитат из книги физика Рудольфа Пайерлса ‘Сюрпризы в теоретической физике‘ (раздел Необратимость).
‘Теперь мы займемся одним из самых фундаментальных вопросов статистической механики, ответ на который известен давно, но недостаточно ясен широкому кругу физиков, по-видимому, даже сегодня. Это — вопрос об истинном происхождении необратимости в статистической механике.’
‘Можно предположить, что эти факты каким-то образом связаны со способом функционирования нашего мозга, но мы не умеем объяснить природу этой однонаправленности.’
‘«Стрела времени» оказывается свойством нашего мозга.’
Проблемы с субъективностью энтропии связаны с вероятностным подходом, — все зависит от истолкования появления вероятности при рассмотрении поведения детерминированной системы. Я не буду на них останавливаться, только отмечу наглядность объяснения стрелы времени по Больцману. По всей видимости поэтому авторы научно-популярных книг его используют. Так, в книге Шона Кэррола ‘Вечность. В поисках окончательной теории времени‘ рассмотрение стрелы времени проведено аналогичным образом, как в книге Пенроуза, правда, в отличие от Пайерлса Кэрролл отстаивает объективность энтропии.
С другой стороны, важно отметить, что подход Больцмана был ограничен рассмотрением идеального газа и поэтому непонятно, как провести в жизнь программу, озвученную Пенроузом выше в общем случае. В методе Больцмана был переход от фазового пространства всей системы к фазовому пространству отдельной частицы; я не видел других путей подсчета числа микросостояний и объема соответствующего фазового пространства. В то же время такой переход ограничен случаем идеального газа, поскольку в данном случае необходимо предположение, что энергия системы является суммой энергий частиц.
В статистической механике используют метод ансамблей Гиббса, который позволяет выйти за рамки идеального газа. Рассмотрению изолированной системы по Больцману соответствует микроканонический ансамбль, в котором для равновесного состояния идеального газа получается сопоставимое выражение для энтропии. Проблема в том, что энтропия по Гиббсу формально не меняется во времени в ходе достижения равновесного состояния — см. следующую заметку.
В заключение про гравитацию. Классическая термодинамика не содержит гравитации, поэтому использование понятия энтропии для вселенной требует изменения формализма классической термодинамики. Положение в статистической термодинамике не лучше. Подход Больцмана ограничен идеальным газов, а при использовании ансамблей практически всегда используется предположение об аддитивности энергии рассматриваемых подсистем. К сожалению, космологи обычно обходят это обстоятельство стороной.
Далее: Энтропия Гиббса в статистической механике
Информация
Роджер Пенроуз, Мода, вера, фантазия и новая физика Вселенной. СПб.: Питер, 2020. Глава 3. Фантазия. Раздел 3.3. Второй закон термодинамики.
Р. Пайерлс, Сюрпризы в теоретической физике. 1988. Глава 3. Статистическая механика. Раздел 3.8. Необратимость.
Roman Frigg, A field guide to recent work on the foundations of statistical mechanics. In The Ashgate companion to contemporary philosophy of physics, pp. 105-202. Routledge, 2016.