Ранее: Введение
Термодинамические свойства, включая энтропию, являются характеристикой вещества; для более точного выражения вводится понятие термодинамической фазы. Фаза в общем случае представляет собой раствор из индивидуальных компонентов, которые также называют чистыми веществами. Рассмотрим сказанное на примере горящей свечи и начнем с воздуха, который окружает горящую свечу. Воздух является газообразной фазой — газовым раствором, содержащим два основных компонента, кислорода (O2) и азота (N2). Последние являются чистыми веществами.
Пламя свечи также представляет собой газовый раствор, только он содержит много компонентов, между которыми протекают химические реакции. Таким образом, состав этого газового раствора в разных зонах пламени отличается друг от друга. Кроме этого, при горении образуются крошечные частички угля, которые придают горению свечи характерный цвет. Таким образом, пламя свечи следует назвать взвесью — газом, в котором распределены маленькие частички твердого вещества. С точки зрения термодинамики говорят о наличии двух фаз — собственно, газовый раствор, и раскаленные частички угля.
Следует обратить внимание, что в термодинамике фаза характеризуется одним характеристическим уравнением состояния и в этом смысле разные частички угля принадлежат одной фазе. При обсуждении этого вопроса следует отделить экстенсивные величины (внутренняя энергия и энтропия) от интенсивных (температура, давление и концентрация). Экстенсивные величины суммируются и таким образом суммарная внутренняя энергия и энтропия всех частичек угля будет суммой по все частичкам, правда в этом случае нельзя забывать о поверхностной энергии.
Материал свечи обычно включает парафин и стеарин; парафин состоит из алканов от C18H38 (октадекан) до C35H72 (пентатриоконтан). Расплав представляет собой гомогенный раствор, то есть, одну термодинамическую фазу, а вот тело свечи имеет сложную структуру композитного материала, содержащего микрочастицы разных фаз. С точки зрения термодинамики следует отсортировать разные микрочастицы по разным термодинамическим фазам; таким образом термодинамика тела свечи будет достаточно сложной.
В книге основное внимание будет уделено термодинамике индивидуального вещества. Тем самым термодинамика растворов и термодинамика тела свечи останутся вне рассмотрения. Также будут проигнорированы поверхностные эффекты — будет считаться, что площадь поверхности фазы пренебрежимо мала. Тем не менее, именно этот уровень обычно используется при сопоставлении термодинамики и статистической механики. Также этого уровня будет достаточно для раскрытия логической структуры термодинамики на уровне представления сплошной среды.
При обсуждении мысленной модели в этой части книги я буду использовать рисунок из книги Сади Карно ‘Размышления о движущей силе огня и о машинах, способных развивать эту силу‘, в которой он предложил знаменитый цикл для поиска максимального коэффициента полезного действия паровой машины:
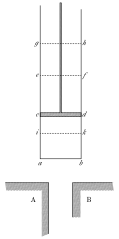
Пока только общее представление о рисунке. На нем изображен цилиндр с поршнем, внутри которого находится вещество. Масса вещества остается постоянной; такая термодинамическая система называется замкнутой. Предполагается, что цилиндр и поршень обладают идеальными термическими свойствами (нулевой теплоемкостью), а также не происходит их деформации. Поэтому считается, что их свойства не влияют на взаимодействие вещества с внешней средой. Поршень задает внешнее давление, а два других тела А и В внизу рисунка будут использованы как термостаты для контроля температуры системы. Когда цилиндр не касается ни одного из этих тел, исключается теплообмен между веществом и окружающей средой. При подсоединении цилиндра к одному из источников теплоты становится возможным теплообмен.
В данном случае будут использованы физические величины из механики без дополнительного рассмотрения: объем (длина), давление и работа, включая методы их измерения. Создание барометров шло параллельно с развитием термометрии, но это принадлежало гидростатике, разделу механики. Поэтому мы начнем с рассмотрения температуры. Эта была первая немеханическая физическая величина и мы рассмотрим, что такое температура в термодинамике и как она связана с термометрией. Также рассмотрим термическое уравнение состояния, которое играет большую роль при рассмотрении термометрии. Важно отметить, что температура играет важную роль во всей механике сплошных сред, поскольку свойства материала являются функцией температуры.
В ходе развития термометрии понятие теплоты было отделено от понятия температуры, что привело к созданию калориметров — приборов для измерения количества теплоты в проводимом процессе. Однако с теплотой все оказалось гораздо сложнее, поскольку теплота не является функцией состояния. Калориметр меряет количество теплоты, но нельзя сказать, что у вещества есть свойство теплота. Последующее развитие оказалось связанным с вопросом о максимальном коэффициенте полезного действия паровой машины и взаимными превращениями теплоты и работы. Вместо теплоты и работы, которые не являются функциями состояния, появились две новые физические величины, внутренняя энергия и энтропия, которые характеризуют состояние вещества.
Мы рассмотрим расчет внутренней энергии и энтропии из экспериментальных данных из уравнения состояния и калориметрии. Правда, для практической работы более удобны новые термодинамические свойства — энтальпия и энергия Гиббса. Будет рассмотрено каким образом из экспериментальных данных составляются термодинамические таблицы, которые в том числе содержат энтропию вещества и которые используются для проведения расчетов равновесного состава.
С другой стороны, классическая термодинамика дает критерии достижения равновесия (неравенство Клаузиуса). Существования неравенства вызывает много вопросов. Так, можно нередко услышать, что классическая термодинамика применима только для равновесных состояний, что по сути дела отвергает неравенство Клаузиуса. Мы рассмотрим на двух простых примерах каким образом в классической термодинамике появляется возможность рассмотрения неравновесных состояний при использовании критериев равновесия.
Термодинамика не содержит времени в явном виде, но во многих случаях это является преимуществом, поскольку дает возможность быстрого решения практических задач. Мы рассмотрим пример оценки температуры пламени свечи, так называемой адиабатической температуры пламени. Здесь потребуется минимальная термодинамика растворов, которая в случае идеального газового раствора будет понятна на интуитивном уровне.
В заключение рассмотрим вопрос энтропии неравновесных состояний в классической термодинамике более подробно, поскольку это потребуется при обсуждении связей между термодинамикой и статистической механикой. В этой главе также будет дан краткий обзор неравновесной термодинамики и рассмотрена ее связь с классической.
Далее: Температура и термическое уравнение состояния
Дополнительная информация
Физическая величина и эмпирический факт: Связь измерения физической величины с теорией физики на примере измерения длины. Наличие погрешности измерения позволяет говорить об эмпирической науке, отделенной от обсуждения картины мира.