Ранее: Глава 4. Неравенство Клаузиуса как критерий равновесия
Классическая термодинамика не содержит времени в явном виде и поэтому периодически встречаются предложения о переименовании ее в термостатику. Такое название однако не включает в себя идеальную тепловую машину Карно, в которой исследовалось превращение теплоты в работы и был найден максимальный коэффициент полезного действия. Аналогичным образом термодинамика дает возможность рассмотрения идеального процесса сгорания без потери тепла и тем самым определить максимально возможную температуру пламени. Название термостатика опять же не включает в себя такую возможность.
В этой главе будет рассмотрен простейший пример — расчет адиабатической температуры пламени при сгорании угля в воздухе. Такой выбор позволяет свести уравнения и вычисления к минимуму, хотя даже в таком случае потребуются дальнейшие упрощения. В любом случае этот пример покажет, что пресловутый недостаток термодинамики — отсутствие времени в явном виде — при решении многих задач превращается в достоинство.
Термодинамика дает уникальную возможность быстрого решения задачи в случае нахождения идеализации, которая предсказывает максимально возможный результат. Напомню, что составление термодинамических справочников было во многом обусловлено задачами оценки тяги ракет, когда расчет адиабатической температуры пламени являлся одной из промежуточных задач на этом пути.
Мы начнем с общей постановки задачи расчета адиабатической температуры пламени. После ее обсуждения будет рассмотрен простейший вариант расчета при полном протекании реакции, а затем будет проведен более сложный вариант с расчетом равновесного состава при заданных температуре и давлении. В заключение я вернусь к словам Эйнштейна про феноменологические теории и рассмотрю с этой точки зрения формализм Гиббса, который лежит в основе современной химической термодинамики.
- Общая постановка задачи
- Расчет температуры пламени при полном протекании реакции
- Расчет равновесного состава при заданных температуре и давлении
- От цикла Карно к химической термодинамике.
Общая постановка задачи
Запишем реакцию сгорания угля в воздухе:
C(уголь) + O2 = CO2
В воздухе также находится азот (N2), который не участвует в реакции, но его присутствие будет влиять на конечную температуру. Для начала рассмотрим мысленную модель, которая будет рассматриваться в этой главе. Рисунок Карно будет снова полезен для визуализации постановки задачи:
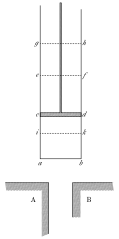
В цилиндре под поршнем, находится изучаемая система — уголь и воздух. В отличие от предыдущего рассмотрения в цилиндре под поршнем будет проходить химическая реакция и таким образом в этой главе мы выйдем за рамки рассмотрения индивидуального вещества. Внешнее давление над поршнем остается постоянным — возьмем одну атмосферу, это будет соответствовать стандартному давлению в справочнике ‘Термодинамические свойства индивидуальных веществ‘. В то же время цилиндр остается не подключенным к источникам теплоты — возможна работа расширения, но теплообмен при этом исключен. Такой процесс называется адиабатическим и в нашем случае он соответствует горению без потери тепла.
Сравним сказанное с горением свечи. В качестве начального состояния выступает тело свечи и воздух при комнатной температуре (в этой главе будет использована температура 25°C=298.15 K). Полный процесс горения проходит достаточно быстро и идеализация сводится к тому, что потери теплоты во время горения игнорируются. Реальная температура пламени будет меньше адиабатической температуры, разница будет связана с процентом потерь энергии в ходе теплообмена с внешней средой. Другая идеализация связана с предположением либо о полном протекании реакции, либо о достижении полного равновесия. Эти предположения приводят к дополнительному отличию адиабатической температуры пламени от реальной температуры.
Неравенство Клаузиуса остается в качестве критерия достижения равновесия в адиабатическом процессе. Самопроизвольный процесс горения в сопровождается увеличением энтропии при постоянной энтальпии и давлении:
(dS)H,p > 0
При достижении равновесия энтропия всей системы достигает максимума. Отличие от изолированной системы заключается в постоянстве других внешних величин — энтальпия и давление вместо внутренней энергии и объема.
Правда, этот критерий не будет непосредственно использован в расчетах ниже. Вначале мы рассмотрим полное протекание реакции и нам потребуется только постоянство энтальпии, поскольку условие полного протекания реакции задает конечное состояние. Далее мы рассмотрим влияние диссоциации углекислого газа, но в этом случае использование критерия равновесия выше приводит к слишком сложным выкладкам; для простоты я ограничусь расчетом равновесия при постоянном давлении и температуре.
Расчет температуры пламени при полном протекании реакции
Начнем с предположения, что реакция сгорания угля проходит полностью; также выберем начальное состоянии, в котором количество воздуха находится в стехиометрическом соотношении с углеродом. Выбор такого начального состояния также влияет на конечные результаты; при оценке температуры реального пламени требуется знание начального состава. В сделанном предположении реакция ниже задает начальное и конечное состояние; число молей азота соответствует отношению азота к кислороду в воздухе:
C(уголь) + O2 + 3.76N2 = CO2 + 3.76N2
Начальное состояние веществ берется при температуре 25°C=298.15 K, конечное — при температуре, которую требуется определить и которая является оценкой температуры процесса горения. Суммарное давление остается равной 1 атм, но парциальные давления газов будут отличаться от одной атмосферы. Все газы будут считаться идеальными, в этом случае энтальпия газа не зависит от давления. Поэтому для расчетов можно использовать стандартные энтальпии при 1 атм. Расчет проведем для одного моля угля, но этот выбор не влияет на конечную температуру.
Изменение суммарной энтальпии равно нулю и это условие будет использовано для определения неизвестной температуры в конечном состоянии (T2). Поскольку изменение энтальпии не зависит от пути перехода, можно выбрать наиболее удобный путь для использования термодинамических таблиц. Представим путь перехода в виду двух стадий: 1) протекание химической реакции при T1 = 298.15 K, 2) нагревание продуктов реакции от 298.15 K до T2. Сумма изменения энтальпии в обоих стадиях равна нулю:
∆rH°(T1) + H°(T2, продукты) − H°(T1, продукты) = 0
В этом уравнении энтальпия реакции при T1 = 298.15 K рассчитывается через энтальпии образования участников реакции. Азот в данном случае не требуется, поскольку он остается в том же самом состоянии:
∆rH°(T1) = ∆fH°m(CO2, T1) − ∆fH°m(C, уголь, T1) − ∆fH°m(O2, T1)
Изменение энтальпий при нагревании следует расписать через изменение энтальпии каждого вещества:
∆H°(продукты) = [H°m(CO2, T2) − H°m(CO2, T1)] + 3.76[H°m(N2, T2) − H°m(N2, T1)]
Для вычисления изменения энтальпии вещества при нагревании следует взять интеграл по теплоемкости, который ниже для простоты будет заменен на произведение средней теплоемкости на разницу температур:
∆H°(продукты) = Cp°m(CO2)(T2 − T1) + 3.76Cp°m(N2)(T2 − T1)
Все вместе взятое дает расчетное уравнение для конечной температуры; энтальпия реакции при T1 тратится на нагревании продуктов реакции от T1 до T2:
T2 = −∆rH°(T1)/[Cp°m(CO2) + 3.76Cp°m(N2)] + T1
В таблице ниже приведены термодинамические данные, необходимые для проведения расчета; энтальпия образования в кДж/моль, энтропия и теплоемкость в Дж/(моль К). В справочнике были данные только для графита, поэтому расчет будет проведен для него, разница с углем невелика.
| С(гр) | O2 | CO2 | N2 | |
| ∆fH°(298.15 K) | 0 | 0 | -393.5 | 0 |
| Cp°(298.15 K) | 8.5 | 29.4 | 37.1 | 29.1 |
| Cp°(1000 K) | 21.7 | 34.9 | 54.3 | 32.7 |
| Cp°(2000 K) | 24.9 | 37.8 | 60.4 | 36.0 |
| S°(298.15 K) | 5.7 | 205.0 | 213.7 | 191.5 |
| S°(2518 K) | 46.6 | 277.5 | 323.2 | 260.3 |
Из данных таблицы получается оценка адиабатической температуры пламени сгорания графита в стехиометрическом количестве воздуха при использовании теплоемкостей при 1000 К в качестве средних значений:
T2 = 393500/(54.3 + 3.76*32.7) + 298.15 = 2518 K
Для расчета не требовались энтропии, но можно проверить, что энтропия конечного состояния больше, чем энтропия начального состояния. Графит является твердой фазой, находящейся под суммарным давлением одна атмосфера и поэтому для него можно использовать стандартную энтропию. В отличии от энтальпии энтропия идеального газа зависит от давления:
S(T, p) = S°(T) − R ln (p/p°)
В нашем случае это влияет на энтропию газов, поскольку газы вместе находятся под давлением одна атмосфера, но в уравнении для энтропии следует использовать парциальное давление газа, которое можно вычислить через мольную долю, приведу уравнение для азота:
p(N2) = x(N2)p°
К счастью в нашей задаче мольная доля азота не меняется, а мольная доля CO2 в конечном состоянии равна мольной доле кислорода в начальном состоянии. Это приводит к тому, что необходимые поправки на измерение парциального давления в начальном и конечном состоянии одни и те же и поэтому они при вычитании взаимно уничтожаются. Таким образом, можно для расчета использовать стандартные энтропии газов:
S2 − S1 = 323.2+3.76*260.3−(5.7+205+3.76*191.5) = 371.2
Расчет выше подтверждает ожидаемый результат — сгорание графита в воздухе в закрытой адиабатической системе при постоянном давлении является самопроизвольным процессом.
Расчет равновесного состава при заданных температуре и давлении
Тем не менее, вычисленное выше изменение энтропии не является максимальным. Дело в том, что при высоких температурах становится заметной диссоциация газов. В нашем случае достаточно только учесть диссоциацию углекислого газа, поскольку концентрации других образующихся компонентов пренебрежимо малы:
| CO2 | = | СO | + | 0.5O2 |
| 1 − ξ | ξ | 0.5ξ |
Возьмем в начальном состоянии один моль CO2; химическая переменная ξ показывает число молей распавшегося CO2 и одновременно число молей появившихся продуктов диссоциации. Задача расчета равновесного состава сводится к нахождению величины химической переменной, соответствующей состоянию равновесия. Азот не включен в уравнение химической реакции, но про него нельзя забывать, поскольку его наличие смещает положение равновесия.
К сожалению, использование критерия максимума энтропии приводит к сложным выкладкам — требуется нахождение двух неизвестных (температура и химическая переменная), а также учет зависимости энтропии от температуры. Поэтому я ограничусь демонстрацией расчета равновесного состава при постоянной температуре и давлении. Мы возьмем конечное состояние реакции при сгорании одного моля графита — один моль углекислого газа при 2518 K и 1 атм — и рассчитаем величину химической переменной в реакции диссоциации до достижения равновесия при этих условиях.
Рассмотрение критерия равновесия в этом случае начну с основного неравенства из предыдущей главы ‘Неравенство Клаузиуса как критерий равновесия‘. Оно определяет протекание самопроизвольного процесса в системе при постоянном внешнем давлении и температуре:
dU − TexdS + pexdV < 0
При рассмотрении системы, находящейся в температурном и механическом равновесии с окружением, то есть, системы с однородной постоянной температурой и давлением, левую часть можно заменить на изменение энергии Гиббса системы:
d(U − TS + pV) < 0 => (dG)T,p < 0
Таким образом энергия Гиббса системы является критерием самопроизвольного протекания процессов при постоянных температуре и давлении внутри рассматриваемой системы и как следствие критерием расчета равновесного состояния — минимум энергии Гиббса рассматриваемой системы при заданных условиях.
Рассматриваемая система состоит из газового раствора (азот, углекислый газ, кислород и оксид углерода). В приближении идеального газового раствора суммарная энергия Гиббса является суммой по компонентам и содержит одну неизвестную — химическую переменную:
G(ξ) = 3.76 Gm(N2) + (1 − ξ)Gm(CO2) + ξGm(CO) + 0.5ξGm(O2)
Правда, энергия Гиббса отдельного компонента в этом случае зависит от парциального давления компонента, которое рассчитывается как произведение мольной доли на общее давление:
Gm,i = G°m,i + RT ln[xi(ξ) p°]
Мольная доля, как и число молей, является функцией химической переменной. Подстановка в исходное выражение и отброс слагаемых, которые не зависят от химической переменной (они не влияют на нахождение минимума), дает расчетное выражение ниже:
G(ξ) = ξΔrG° + RT[(1 − ξ) ln p(CO2) + ξ ln p(CO) + 0.5ξ ln p(O2) + 3.76 ln p(N2)]
В нем парциальные давления являются функциями химической переменной, а ΔrG° является стандартной энергией Гиббса реакции диссоциации углекислого газа, которую можно рассчитать из термодинамических таблиц для данной температуры: ΔrG°(2518 К) = 67.4 кДж/моль. График функции, построенный в Gnuplot (см. код в Приложении), показан ниже. Он позволяет оценить значение химической переменной, для которого достигается минимум энергии Гиббса (точное значение ξ = 0.213).
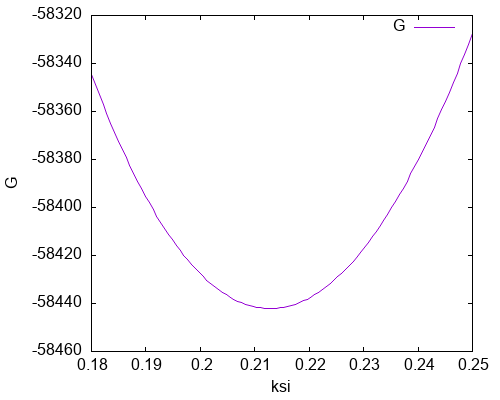
Приведенный график также хорошо демонстрирует разницу между локальным и глобальным равновесием. Любое значение химической переменной характеризует газовый раствор, находящийся в локальном термическом и механическом равновесии — все вещества находятся при заданной температуре и сумма парциальных давлений равна внешнему давлению. В то же время химическое равновесие достигается только в точке минимума энергии Гиббса.
Справочное значение стандартной энтальпии реакции диссоциации углекислого газа при этой температуре равно ΔrH°(2518 К) = 275.1 кДж/моль. Равновесное значение химической переменной показывает, что из энтальпии, выделившейся при сгорании графита (393.5 кДж), часть 275.1*0.213 = 58.6 кДж уйдет на диссоциацию CO2. Тем самым на нагрев компонентов останется меньше энергии, что в свою очередь приведет к уменьшению адиабатической температуры пламени.
Использование критерия максимума энтропии позволяет одновременно определить равновесный состав и температуру, но выкладки на этом пути достаточно сложны. В Дополнительной информации содержится ссылка на заметку с вычислением замерзания переохлажденной воды — в ней можно найти использование этого критерия в случае более простой задачи. С другой стороны, можно предложить итеративный способ решения. Требуется сделать поправку на найденное значение энтальпии, необходимой для диссоциации. Это даст новую оценку адиабатической температуры пламени, теперь можно провести при этой температуре расчет равновесного состава, использовать новую поправку на найденную энтальпию, необходимую для диссоциации и т.д. до достижения сходимости.
От цикла Карно к химической термодинамике
В настоящее время название химическая термодинамика включает в себя детальное рассмотрение растворов, а также химические и фазовые превращения — все это осталось за пределами этой книги. Важно отметить, что формализм современной химической термодинамики был создан физиком Джозайя Виллардом Гиббсом в классической работе ‘О равновесии гетерогенных веществ‘ в 1876-1878 гг. Правда, потребовалось значительное время для осознания химиками важности этой работы Гиббса, но в любом случае именно эта работа лежит в основе современной химической термодинамики. Конечно, нельзя забывать об экспериментальных исследованиях, которые необходимы для создания базы данных термодинамических свойств — без этого использование формализма для решения практических задач невозможно. Эта часть по праву называется экспериментальной химической термодинамикой и это результат совместной работы физиков и химиков.
Вспомним характеристику Эйнштейна феноменологической физики как науки ‘близкой к опыту понятий’. Именно в таком смысле классическая термодинамика в настоящее время называется феноменологической. Такое отношение хорошо выражено в статье Вернера Гейзенберга 1966 года ‘Роль феноменологических теорий в системе теоретической физики‘:
‘Конечно, феноменологические теории развиваются всегда там, где наблюдаемые явления еще не могут быть сведены к общим законам природы. Причина этой невозможности может состоять либо в чрезвычайной сложности соответствующих явлений, которая еще не допускает такое сведение из-за математических трудностей, либо в незнании упомянутых законов. … Примеры для второго случая: … в первой половине 19 века — размышления Фарадея об электричестве и феноменологическая термодинамика, в античной астрономии — птолемеевская теория циклов и эпициклов в движении планет.’
Однако введение энтропии в ходе изучения идеальной тепловой машины Карно и формализм Гиббса для расчета химических равновесий никак не вписываются в этой схему — это достаточно неожиданные следствия из законоы классической термодинамики. Точно также общие законы природы, про которые говорит Гейзенберг и которые мы рассмотрим в следующих разделах книги, позволяют связать термодинамические свойства веществ с молекулярным строением, но при этом не позволяют вывести критерий равновесия.
Для обсуждения этого вопроса сделаю небольшое исторические отступление. Протекание химических реакций объяснялось химиками наличием сродства между реагентами. В молекулярно-кинетической теории 19-ого века не было средств для объяснения протекания химических реакций, то есть, рассмотрение процессов горения на этом уровне было невозможно. Калориметрия химических реакций дала первый количественный показатель оценки химического сродства — теплоту реакции. В начале второй половины 19-ого века химики стали позиционировать теплоту реакции как критерий самопроизвольного протекания химических реакций (принцип Бертло – Томсена).
Гиббс заложил основы современной химической термодинамики, но его не интересовало использование разработанного формализма для решения химических задач. Пьер Дюгем верно распознал силу метода Гиббса и в диссертации 1884 года он показал ошибочность принципа Бертло. Также Дюгем предложил использование метода термодинамических потенциалов во многих областях физической физики. Однако работа Дюгема вызвала раздражение у Бертло и его сторонников, что привело к трудностям в карьерном росте Дюгема как физика. При этом химики не обратили внимание на работы Дюгема — слишком много непонятной физики и математики.
Элементы термодинамики были введены в химию в конце 19-ого — начале 20-ого века Якобом Вант-Гоффом, Сванте Аррениусом и Вильгельмом Оствальдом. Их упрощенный подход больше понравился химикам и шаг за шагом термодинамика проникла в химии. Дальнейшее развитие потребовало использования исходного строгого формализма Гиббса, но этот процесс занял значительное время. В настоящее время преимущества метода Гиббса наиболее видны в случае фазовых диаграмм (см. CALPHAD, CALculation of PHAse Diagrams), когда термодинамика позволяет провести совместную обработку разнородных экспериментов для определения наиболее точных энергий Гиббса фаз и их дальнейшее использование при расчете фазовых диаграмм.
В этом свете будет более понятно значение выражение ‘феноменологическая теория’ в докладе Людвига Больцмана ‘О развитии методов теоретической физики в новейшее время‘ в 1899 году. Больцман начинает рассмотрение феноменологических теорий с теории электромагнитного поля Максвелла:
‘Максвелл рассматривал свою теорию всего только как модель природы, или, по его выражению, как механическую аналогию, которая в данный момент позволяет наиболее полно привести к единству всю совокупность явлений. Мы увидим, что эта позиция Максвелла оказала громадное влияние на дальнейшее развитие теории. Своими практическими успехами Максвелл способствовал быстрой победе этих теоретических идей.’
Более того, Больцман связывает успехи экспериментов Герца, подтверждающих теорию Максвелла, с последующим успехом развития феноменологических теорий:
‘И подобно тому как маятник, проходя свое положение покоя, отклоняется в противоположную сторону, так и экстремисты начали в конце концов говорить об ошибочности всех представлений старой классической теории физики.’
Под старой классической теорией физики Больцман понимает идеал познания ‘истинной природы вещей’. Он таким образом характеризует феноменологические теории:
‘При такой точке зрения задача физики сводилась единственно лишь к тому, чтобы с помощью ряда попыток находить возможно более простые уравнения, удовлетворяющие определенным необходимым формальным условиям, например изотропии и т. д., и затем сравнивать их с опытом. Это и есть крайнее феноменологическое направление, которое я мог бы назвать также математическим, поскольку общая феноменология стремится к описанию всех явлений путем их перечисления и естественнонаучного описания, без какого-либо ограничения используемых для этого средств, но только с отказом от всякого цельного миропонимания, от любого механического объяснения или какого-либо иного обоснования.’
Таким образом Больцман считает феноменологическую термодинамику ничуть не хуже теории электромагнитного поля Максвелла. Более того, согласно логике доклада Больцмана принятие идей феноменологической термодинамики в конце 19-ого века явилось следствием успеха теории Максвелла. С таким значением выражения феноменологическая теория можно было бы согласиться, но такое значение сильно отличается от того, что подразумевается под феноменологической теорией в настоящее время.
Далее: Глава 6. Энтропия неравновесных состояний
Информация
Термодинамические свойства индивидуальных веществ. Справочное издание в четырех томах, третье издание, 1978 — 1982.
Таблицы онлайн: Термодинамические свойства индивидуальных веществ
Больцман, Эйнштейн и Гейзенберг о феноменологической термодинамике: Приведены цитаты из статей. Видение феноменологической теории по ходу развития теории физики. Так, Больцман считал теорию электромагнитного поля феноменологической. Вопрос понимания энтропии.
Дополнительная информация
Замерзание переохлажденной воды: Рассмотрена термодинамика замерзания переохлажденной воды в изолированной системе. Происходит самопроизвольный переход к гетерогенному равновесию из льда и воды при температуре фазового равновесия.
Парадокс Гиббса в классической термодинамике: Обсуждение вопроса, почему в парадоксе Гиббса в классической термодинамике не осталось ничего парадоксального. Обоснование и сравнение с обсуждением в статье Оливье Дарриголя и книги С. Д. Хайтуна.
Приложение
Код Gnuplot для построения графика:
set terminal png enhanced size 500,400
set output 'C_02_C02.png'
R = 8.31441
ptot = 1
T = 2518
DelG = 67400
pN2(ksi) = 3.76/(3.76+1+0.5*ksi)*ptot
pCO2(ksi) = (1-ksi)/(3.76+1+0.5*ksi)*ptot
pCO(ksi) = ksi/(3.76+1+0.5*ksi)*ptot
pO2(ksi) = 0.5*ksi/(3.76+1+0.5*ksi)*ptot
G(ksi) = ksi*DelG+R*T*(3.76*log(pN2(ksi))+(1-ksi)*log(pCO2(ksi))+ksi*log(pCO(ksi))+0.5*ksi*log(pO2(ksi)))
set xlabel 'ksi'
set ylabel 'G'
plot [x=0.18:0.25] G(x) title 'G'