1.4. Неравенство Клаузиуса как критерий равновесия

Содержание книги

Ранее: Глава 3. Термодинамические свойства веществ

Идеализация Карно позволяет найти максимальный коэффициент полезного действия (к.п.д.) тепловой машины; в реальной тепловой машине к.п.д. меньше максимального. Этот факт приводит к появлению неравенства Клаузиуса, которое выражает это обстоятельство на языке энтропии. В классической термодинамике неравенство Клаузиуса задает критерий самопроизвольного процесса и одновременно критерий равновесия — состояния, которым завершается самопроизвольный процесс.

Мы начнем с раздела ‘Неравенство Клаузиуса для изолированной системы‘, а далее рассмотрим простой пример в разделе ‘Простейший пример тепловой смерти‘. Подстановка неравенства Клаузиуса в первый закон будет рассмотрена в разделе ‘Основное неравенство термодинамики‘, в котором также будет дан простой пример использования основного неравенства в случае достижения равновесия идеального газа. Эти простые примеры покажут, каким образом в классической термодинамике возможно рассмотрение неравновесных состояний.

В последнем разделе ‘Локальное и глобальное равновесие. Построение термодинамики‘ случаи неравновесных состояний в рассмотренных примерах будут обобщены на более сложные неравновесные состояния. Также будет затронуто обстоятельство, которое я упоминал при рассмотрении температуры. Введение температуры уже требует условия достижение теплового равновесия, поэтому следует рассмотреть общий критерий равновесия на основе неравенства Клаузиуса в этом свете.

Неравенство Клаузиуса для изолированной системы

Неравенство во втором законе термодинамики (неравенство Клаузиуса) вызывает особые трудности при изучении классической термодинамики. Ниже я выпишу только часть второго закона, связанную с неравенством:

dS > dQ/T_ex

Для простоты представим себе изолированную систему без обмена энергией с окружением — отсутствует теплообмен и не совершается работа. Это означает, что внутренняя энергия и объем остаются постоянными и таким образом неравенство Клаузиуса выглядит следующим образом:

(dS)_U,V > 0

Нижние индексы подчеркивают условие постоянства внутренней энергии и объема, про это нельзя забывать. В этих условиях неравенство Клаузиуса становится критерием самопроизвольного процесса в изолированной системе — энтропия изолированной системы может только возрастать. Отсюда следует, что при достижении равновесия протекание самопроизвольного процесса прекращается, а энтропия достигает максимума при заданных значениях внутренней энергии и объеме.

В этот момент возникает определенная логическая проблема. Из утверждения о максимуме энтропии при достижении равновесия следует, что в классической термодинамике есть средства для работы с неравновесными состояниями. С другой стороны можно услышать, что равенство во втором законе можно использовать только для равновесных процессов — то есть, в классической термодинамике нельзя говорить об энтропии неравновесных состояний.

Этот вопрос упирается в многозначность термина неравновесное состояние. Мы начнем с простых примеров, в которых будет показано, что, как минимум, в классической термодинамике есть средства для работы с некоторыми неравновесными состояниями, а в последующем это утверждение будет обобщено на более сложные неравновесные состояния.

Простейший пример тепловой смерти

Начнем с простейшего примера, когда изолированная система состоит из двух подсистем, с одинаковой теплоемкостью (C_V,1 = C_V,2), не зависящей от температуры. Две подсистемы отделены друг от друга неподвижной перегородкой — индекс 0 характеризует начальные значения температур:

$$T_{1,0}\mid T_{2,0}$$

Объемы подсистем не меняются и единственная возможность изменений связана с температурами подсистем — перегородка пропускает теплоту. Примем, что переход внутренней энергии в виде теплоты происходит крайне медленно и что в обоих подсистемах не возникает градиентов температур. Другими словами, обе подсистемы находятся в состоянии локального равновесия с однородными температурами.

Полная система с другой стороны не находится в состоянии равновесия, поскольку возможен обмен энергией между подсистемами. Задачей становится рассмотрение всех возможных состояний полной системы. По условию задачи изменения внутренней энергии подсистем должны быть равны между собой с обратным знаком (полная энергия сохраняется: U = U₁ + U₂ = const), что в случае одинаковых теплоемкостей приводит к простому соотношению между температурами:

$$d{U}_1=—d{U}_2$$ $$C_{V}d{T}_1=—C_{V}d{T}_2$$ $$T_1=T_{1,0}+x\mid T_2=T_{2,0}—x$$

Переменная x показывает возможные изменения температур, повышение температуры в одной подсистеме равно понижению температуры в другой, поскольку теплоемкости одинаковы. Суммарная внутренняя энергия от x не зависит, поскольку постоянство суммарной внутренней энергии заложено в вывод последнего соотношения.

В то же время суммарная энтропия зависит от значений текущих температур в подсистемах, то есть, от значения x. В уравнении ниже взят интеграл энтропии при изменении температуры, а S₀ обозначает суммарную энтропию в начальном состоянии:

$$S=S_1+S_2=S_0+C_{V}ln\frac{T_1}{T_{1,0}}+C_{V}ln\frac{T_2}{T_{2,0}}$$ $$S=S_0+C_{V}ln\frac{T_{1,0}+x}{T_{1,0}}+C_{V}ln\frac{T_{2,0}—x}{T_{2,0}}$$

Перед последним шагом рассмотрим график функции зависимости суммарной энтропии от x. Он построен для случая начальных температур 300 К и 400 К, при этом S₀=0, C_V=1.

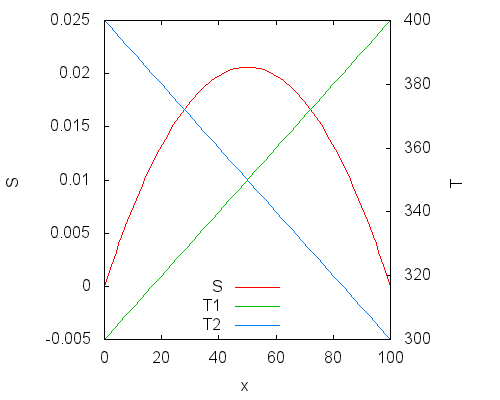
Изменение температуры показано на правой оси ординат: T₁ = 300 + x, T₂ = 400 ‐ x, изменение энтропии на левой. Энтропия достигает максимума при x = 50, когда температуры подсистем становятся равными. Это согласуется с ожиданиями — равновесное состояние всей системы соответствует термическому равновесию между подсистемами.

Максимум энтропии соответствует равенству нулю производной энтропии, это позволяет получить ответ в общем виде:

$$dS/dx=0,x=\left(T_{2,0}—T_{1,0}\right)/2$$ $$T_{2,eq}=T_{1,eq}=\left(T_{2,0}+T_{1,0}\right)/2$$

Итак, значение неравновесного состояния в этом примере связано со случаем, когда изолированная система состоит из подсистем, каждая из которых имеет однородные температуры. Подсистемы сами по себе находятся в равновесном состоянии, но они не находятся в равновесии друг с другом.

Важно отметить, что установление равновесия во всей системе является следствием второго закона термодинамики, поскольку изменение x на графике во всем интервале возможных значений не нарушает первый закон. Поэтому изменение энтропии в изолированной системе связывают со стрелой времени; как уже упоминалось, возрастание энтропии в изолированной системе задает направление самопроизвольных процессов.

На языке тепловых машин неравенство Клаузиуса выражает отсутствие полной эквивалентности работы и теплоты. Всю работу можно превратить в теплоту, но только часть теплоты можно превратить в работу. В изолированной системе, которая включает в себя тепловую машину и окружающие тела, самопроизвольные процессы приводят к потере возможности совершения работы. Полная энергия сохраняется, но при достижении полного равновесия в изолированной системе теряется возможность совершения работы.

Рассмотренный пример допускает пессимистическое истолкование в виде так называемой тепловой смерти вселенной. Рудольф Клаузиус после введения энтропии не упустил возможность перенести сказанное на всю вселенную: ‘Die Energie der Welt ist konstant. Die Entropie der Welt strebt einem Maximum zu. (Энергия мира постоянна, энтропия мира стремится к максимуму)’. Это классический пример экстраполяционизма, когда результаты исследования частного случая (тепловой машины) без промедления и колебаний переносятся на весь мир.

Основное неравенство термодинамики

При объединении неравенства Клаузиуса с первым законом получается основное неравенство классической термодинамики:

dU < T_exdS — p_exdV

В неравенство входит внешняя температура и давление, которые фиксированы и поэтому уже не являются функциями энтропии и объема системы. Именно это обстоятельство приводит к тому, что основное неравенство существенно отличается по смыслу от основного уравнения термодинамики, рассмотренного в предыдущей главе. Основное уравнение описывает изменение термодинамических свойств вещества в пространстве независимых переменных, а основное неравенство является критерием самопроизвольности процесса в ходе достижения равновесия при заданных внешних условиях. Для лучшего понимания рассмотрим снова рисунок Сади Карно:

Представим следующую ситуацию. Вещество при однородных температуре и давлении (T₁, p₁) находилось в цилиндре. Далее цилиндр подключили к источнику теплоты с температурой T_ex и изменили внешнее давление на p_ex. В этот момент начинается самопроизвольный процесс перехода вещества из начального состояния в конечное. Для его рассмотрения удобно перенести все слагаемые в левую часть неравенства:

dU — T_exdS + p_exdV < 0

Это задает функцию, которая в самопроизвольном процессе может только уменьшаться и которая при достижении конечного равновесного состояния будет минимальна. Таким образом критерий самопроизвольного процесса одновременно является критерием достижения конечного равновесного состояния (минимальное значение функции в левой части неравенства).

В классической термодинамике в конечном равновесном состоянии всегда получается однородные температура и давления, когда все градиенты исчезают. Поэтому я упрощу задачу и при рассмотрении неравенства выше я ограничу рассмотрение состояниями рабочего тела с однородными температурой и давлением. Задача станет такой — при рассмотрении всех возможных состояния рабочего тела с однородными температурами и давлениями найти равновесное состояние, которое соответствует заданным условиям.

Интуитивно ответ понятен, но давайте увидим формально, что неравенство выше согласуется с интуитивными ожиданиями — что его применение приводит к установлению термического и механического равновесия. Кстати, это демонстрирует относительность понятия равновесного состояния — состояние с однородной температурой и давлением может быть равновесным, но в данном рассмотрении оно является неравновесным по отношению к внешним условиям.

В рассматриваемой задаче при заданных ограничениях можно заменить dU в неравенстве на выражение из основного уравнения, поскольку оно применимо для описания изменений между состояниями с однородной температурой и давлением. Это дает следующее выражение

(T — T_ex)dS + (p_ex — p)dV < 0

Теперь должно стать понятнее, что минимум функции слева будет достигаться при достижении рабочим телом температуры и давления, равным внешним давлению и температуры, то есть, неравенство в конечном итоге приведет к критерию термического и механического равновесия. Для наглядности сделаю ниже вычисление левой части в случае одного моля идеального газа: pV = RT (R — универсальная газовая постоянная). Для удобства переведу неравенство в пространство состояний температура — объем, поскольку в этих переменных получаются наиболее простые выражения для расчета. Для этого использую выражение энтропии как функцию от этих независимых переменных:

$$dS=\frac{C_V}{T}dT+{\left(\frac{\partial p}{\partial T}\right)}_{V}dV=\frac{C_V}{T}dT+\frac{R}{V}dV$$

Первая часть уравнения относится к любому телу; C_V — теплоемкость при постоянном объеме, которая ниже будет считаться независимой от температуры. Вторая часть уравнения получена вычислением производной по уравнению состояния идеального газа. Подстановка в неравенство плюс использование уравнения состояния идеального газа плюс выкладки приводит к выражению неравенства в случае одного моля идеального газа:

$$\left(T—T_{ex}\right)\frac{C_V}{T}dT+\left(\frac{R{T}_{ex}}{V_{ex}}—\frac{R{T}_{ex}}{V}\right)dV<0$$

Поскольку переменные оказываются разделенными, можно взять интеграл при переходе из состояния (V₁, T₁) в (V₂, T₂), что дает конечное расчетное выражение:

$$C_V\left(T_2—T_1\right)—T_{ex}{C}_{V}ln\frac{T_2}{T_1}+\frac{R{T}_{ex}}{V_{ex}}\left(V_2—V_1\right)—{RT}_{ex}ln\frac{V_2}{V_1}<0$$

В этом выражении (V₁, T₁) относятся к начальному состоянию в примере, (V_ex, T_ex) — к внешним условиям, (V₂, T₂) является промежуточным состоянием. Неравенство говорит, какие промежуточные состояния допустимы с точки зрения законов термодинамики при переходе из (V₁, T₁) в (V_ex, T_ex), а также в каком случае достигается минимум функции слева. Напомню, что минимальное значение функции будет соответствовать равновесному состоянию относительно заданных внешних условий (V_ex, T_ex). Ниже представлен контурный график для функции в левой части неравенства для двух фиксированных точек (V₁, T₁) и (V_ex, T_ex) как функция промежуточного состояния (V₂, T₂):

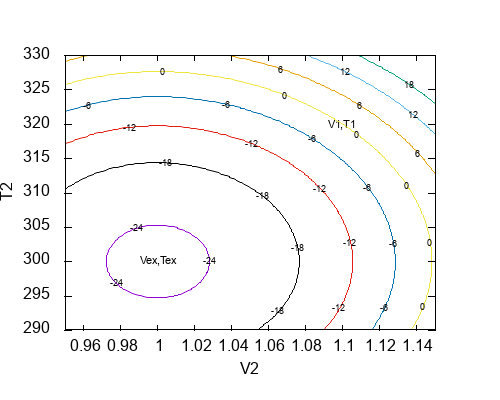
Как и следовало ожидать, функция достигает минимума в (V_ex, T_ex); это будет конечным равновесным состояниям. Положительные значения неравенства показывают, что в данных условиях самопроизвольный переход из (V₁, T₁) в эту область термодинамически невозможен. Рабочее тело может самопроизвольно переходить только в сторону уменьшения функции в левой части неравенства. В то же время неравенство не позволяет вычислить путь перехода, а также оно не содержит информации о времени перехода. Неравенство только позволяет классифицировать возможные состояния при переходе из (V₁, T₁) в (V_ex, T_ex) на термодинамически допустимые и термодинамически недопустимые, а также оно говорит, что минимальное значение соответствует равновесному состоянию.

Локальное и глобальное равновесие. Построение термодинамики

В двух рассмотренных примерах использовалась подсистема с однородной температурой и давлением. Неравновесное состояние получалось при контакте двух подсистем или контакте одной подсистемы с внешними условиями. Это показывает относительность понятия ‘равновесное состояние’ — подсистема может быть в равновесном состоянии сама по себе, а неравновесность вызывается контактами этой подсистемы с другими подсистемами или внешними условиями. В этом случае следует отличать локальное равновесие от глобального. Глобальное неравновесное состояние всей системы разбивается на подсистемы, каждая из которых находится в локальном равновесии. Далее подсистемы в локальном равновесии обмениваются энергией между собой и с внешними условиями до достижения полного равновесия между всеми подсистемами и внешними условиями. Такое состояние будет называться глобальным равновесием.

В рассмотренных примерах всю систему можно назвать прерывной — она состоит из подсистем, в каждой из которых температура однородна. Можно обобщить такое рассмотрение на случай одной системы с полем температур путем разбиения исходной системы на бесконечно малые подсистемы. Таким образом, в классической термодинамике вполне есть средства работы с неравновесными состояниями при использовании принципа локального равновесия.

Введение локального и глобального равновесия также решает одну из проблем в построении термодинамики. При рассмотрении понятия температуры обращалось внимание, что введение температуры уже требует допущения об установлении теплового равновесия между термометром и системой. Точно также при рассмотрении первого закона неявно использовалось допущение об установлении механического равновесия после движения поршня. Правда, последнее являлось естественной частью механики, в которую всегда закладывалось установление статического равновесия.

Следует сказать, что при построении термодинамики были использованы принципы локального равновесия, а неравенство Клаузиуса и основное неравенство термодинамики дает формулировку критериев глобального равновесия. При этом критерии глобального равновесия приводят к следствиям, которые невозможно вывести непосредственного из принципа локального равновесия без введения первого и второго закона. Например, использование критериев глобального равновесия в применении к химическим и фазовым равновесиям содержится в классической работе Гиббса ‘О равновесии гетерогенных веществ‘ 1876-1878 гг. Работа Гиббса лежит в основе обсуждения направление протекания химических реакций и тем самым она играет роль в понимании процесса горения свечи.

В то же время при обсуждении вопроса стрелы времени нельзя забывать, что установление теплового равновесия является пререквизитом классической термодинамики, а установление механического равновесия является пререквизитом механики сплошных сред. Таким образом, строго говоря, второй закон в классической термодинамике показывает направление установления глобального равновесия при условии существования локального равновесия.

В этом свете несколько слов про аксиоматизацию. Можно увидеть попытки упростить построение термодинамики исходя из принципа глобального равновесия. Вначале вводятся внутренняя энергия и энтропия, а затем температура определяется как производная внутренней энергии по энтропии: T = (∂U/∂S)_V. Например, см. аксиоматизацию в статье Либа и Ингвасона 1999 года — Lieb&Yngvason ‘The physics and mathematics of the second law of thermodynamics‘.

С моей точки зрения такое построение термодинамики проблематично, поскольку непонятно, как в нем ввести в рассмотрение поле температур, а также поле давлений. Без этого в свою очередь становится непонятно, как можно использовать неравенство Клаузиуса, которое предполагает наличие определенных средств для работы с неравновесными состояниями. Мы вернемся к рассмотрению этих вопросов в последней главе ‘Неравновесные состояния и энтропия‘, где будет также рассмотрена связь между классической и неравновесной термодинамикой.

Далее: Глава 5. Адиабатическая температура пламени

Информация

Законы термодинамики. Простейший пример тепловой смерти: Законы термодинамики и уравнения для расчета изменения внутренней энергии и энтропии. На простейшем примере рассмотрено использование энтропии для расчета равновесного состояния в изолированной системе.

Неравенства в классической термодинамике: Рассмотрение основного закона термодинамики и неравенства, связанного с ним. Приведен расчетный пример использования неравенства при вычислении достижения равновесия в случае идеального газа.

Дополнительная информация

Неравенство Клаузиуса, второй закон и стрела времени: Критика статьи Йоса Уффинка ‘Блефуйте по-своему во втором законе термодинамики‘. Обосновывается связь второго закона в виде неравенства Клаузиуса со стрелой времени.

Глобальное и локальное тепловое равновесие в классической термодинамике: Обоснование и аксиоматизация классической термодинамики. Отличие между локальным и глобальным термическим равновесием. Формулировка Клаузиуса и неравновесные состояния в классической термодинамике.

Обсуждение

https://evgeniirudnyi.livejournal.com/401845.html