Содержание книги, книга в формате pdf
Ранее: Глава 2. Математика и мир в механике сплошных сред
Молекулярно-кинетическая теория предложила унифицированный взгляд на разнообразные процессы в механике сплошных сред. Приведу часть цитаты Эйнштейна (см. раздел ‘Эйнштейн о феноменологических и фундаментальных теориях физики‘ во ‘Введении‘):
‘Первая [кинетическая теория газов] объединила уравнение состояния идеальных газов, вязкость, диффузию газов и установила логическую связь между явлениями, которые, с точки зрения прямого опыта, не имели абсолютно ничего общего. … Кинетическая теория … намного обогнала феноменологическую физику [подразумевается механика сплошных сред] в том, что касается логического единства своих основ.’
Эти представления основаны на математических уравнениях теории физики, но философия физики Людвига Больцмана дает возможно качественных объяснений на уровне использования математических очков. Больцман предлагает нейтральное рассмотрение использования математики в физике, когда молекулярно-кинетическая теория рассматривается как наглядный образ для объяснения механики сплошных сред. В то же время проекция такой концептуальной модели на мир крайне затруднена; даже на уровне атомизма 19-ого века невозможно сказать, что такое материя без математических очков.
Далее рассмотрена связь концептуальных моделей статистической механики с экспериментами и тем самым будет затронута проблема координации. Мы рассмотрим спектроскопию, появившуюся в 19-м веке, а также экспериментальное определение фундаментальных постоянных; именно эти эксперименты смогли убедить физиков в реальности существования атомов в начале 20-го века. Квантовая механика смогла объяснить спектры и тем самым открыла путь к использованию суммы по состояниям в статистической механике (см. главу 2.2 ‘Равновесная статистическая механика‘).
В ходе развития физики появились разные уровни аппроксимации, рассмотренные в главе 2.1 ‘Мысленные модели статистической механики‘. В этой главе рассмотрены два примера: колебательное движение двухатомных молекул как пример объяснения теплоемкости газа и ансамбль Гиббса как путь введения частотной интерпретации вероятности. Оба примера соответствуют духу картинки-представления Больцмана: создается наглядная модель, способствующая пониманию. В то же время вопрос перенос этих представлений на мир без использования математических очков невозможен.
- Философия физики Людвига Больцмана
- Концептуальная модель молекулярно-кинетической теории
- Спектроскопия
- Фундаментальные постоянные
- Квантовая механика и расчет из первых принципов
- Колебательное движение в двухатомных молекулах
- Ансамбль Гиббса и вероятности
Философия физики Людвига Больцмана
Людвиг Больцман предлагал философию физики под названием Bildtheorie (картина-представление). Идеи Больцмана хорошо изложены в статье де Регта ‘Картины-представления Людвига Больцмана и научное понимание‘ и поэтому я ограничусь только выразительными цитатами Больцмана:
О значении теорий (1890)
‘Я держусь мнения, что задача теории заключается в конструировании существующего исключительно в нас отражения внешнего мира, которое должно служить путеводной звездой во всех наших мыслях и экспериментах, т.е. заключается, так сказать, в завершении мысленного процесса и выполнении в большем масштабе того, что в малом совершается в нас при образовании каждого представления.’
Памяти Йозефа Лошмидта (1895)
‘Конечно, наши молекулярно-теоретические понятия существуют только внутри нас; однако явления, соответствующие им, существуют независимо от нас, вне нас, и если сегодня, вместо того, чтобы сказать «молекулы существуют», мы предпочитаем говорить «наши соответствующие представления являются простой и целесообразной картиной наблюдаемых явлений», то новый способ выражения может иметь известное преимущество, но по существу и при старом способе имели в виду совершенно то же самое.’
О неизбежности атомистики в естественных науках (1897)
‘В то время как феноменология для изложения механики движений центра тяжести и движения твердых тел, для теории упругости, гидродинамики и т. д. нуждается в отдельных, мало между собой связанных образах, современная атомистика представляет собой совершенно точную картину всех механических явлений. При замкнутости этой области едва ли можно ожидать, что в ней будут открыты какие-либо новые явления, не вмещающиеся в рамках этой картины.’
О статистической механике (1904)
‘Я и не думаю отрицать, что эта область содержит много гипотетического; напротив, картина, ею рисуемая, смело выходит за рамки опыта. И тем не менее она заслуживает обсуждения с этой кафедры; так далеко, идет мое доверие к гипотезам, когда они представляют в новом свете известные особенности наблюдаемые явлений и дают столь наглядную картину взаимоотношений между ними, какая недостижима другими средствами.’
Больцман подчеркивает преимущество атомно-молекулярных представлений в единообразном описании самых разных явлений; в идеале все явления механики сплошных сред должны получить объяснение в этих рамках — высказывание Эйнштейна хорошо перекликается со взглядами Больцмана. В то же время Больцман подчеркивает гипотетичность такой картины, что однако не следует рассматривать как уступку противникам молекулярно-кинетической теории. Философия физики Больцмана восходит к философии Герца, которая в свою очередь явилась отражением ‘кризиса силы’ в классической механики в конце 19-го века. Подход Больцмана предлагает нейтральное рассмотрение концептуальных моделей физики и он содержит трактовку качественного объяснения и понимания при использовании математических очков.
Концептуальная модель молекулярно-кинетической теории
В настоящее время молекулярно-кинетической теории соответствует наглядная образная модель классической статистической физики. Однако, даже на уровне атомизма 19-го века были непреодолимые трудности при попытке проекции такой модели на мир. Как следствие, Эмиль Дюбуа-Реймон в лекции ‘О пределах познания природы‘ в 1872 году пришел к выводу о невозможности познания в физике сущности материи. Дюбуа-Реймон исходил из идеала молекулярно-кинетической теории:
‘Представим себе, что все изменения в мире тел были сведены на движения атомов, происходящих от действия их постоянных центральных сил, тогда вселенная была бы познана в естественно-научном отношении. Состояние вселенной в продолжении одного бесконечно малого пространства времени являлось бы нам непосредственным результатом состояния ее в продолжении предыдущего и непосредственной причиной ее состояния в продолжении следующего бесконечно малого пространства времени. Закон и случай были бы тогда лишь другими названиями для механической необходимости.’
Дюбуа-Реймон признает ограниченность человеческого разума, но он предлагает перейти на уровень демона Лапласа и рассмотреть, что демон Лапласа может сказать о материи и сознании; в этом разделе я остановлюсь только на материи. В рассмотрении Дюбуа-Реймона вопрос роли математики в теории физики не обсуждался в явном виде, но ход обсуждения показывал трудности перехода к миру из идеального знания теории физики на уровне математических уравнений.
Демон Лапласа оперирует материальными точками и силами взаимодействия. Это полностью соответствует концептуальной модели классической статистической механики — для определения перехода мира из предыдущего состояния в последующее не требуется ничего другого. Однако, Дюбуа-Реймон доказывает, что попытки представить себе реальный атом в этой картине упирается в неразрешимые противоречия.
В варианте атома в виде материальной точки атом не занимает пространства. Попытка придать атому определенный размер требует решения вопроса, является ли атом упругим или абсолютно твердым. В первом случае требуется введение сил внутри атома, и в конце концов получается исходный вариант с точечной массой и некоторым потенциалом взаимодействия, который плавно переходит из области атома в область пустого пространства. При этом остается неясным процесс нахождения точки перехода, то есть, решения вопроса, где заканчивается атом и начинается пустое пространство.
Вариант с абсолютно твердым атомом также проблематичен, поскольку, с одной стороны, остается непонятно, почему такой шарик нельзя разделить на части, а, с другой, столкновение абсолютно твердых шаров приводит к трудностям на уровне классической механики. Расчет траекторий становится возможном только при использовании законов сохранения, а расчет непосредственного изменения силы в ходе столкновения становится невозможным — возникает парадокс бесконечной силы, действующей на абсолютно твердое тело.
Следующая проблема связана с силами взаимодействия между атомами. Непонятно, что можно сопоставить таким силам в реальности, при этом силы в классической механики являются дальнодействующими. В этом случае нередко переходят к потенциальной энергии взаимодействия, а сила рассматривается как производная. Это ведет к мягкой форме энергетизма (существует материя и энергия), но, по-прежнему, перенос этих представлений на мир без математических очков невозможен.
Введение картинок-представлений Больцмана позволяет избежать этих проблем, поскольку объяснение и качественное рассмотрение остается на уровне концептуальных моделей с использованием математических уравнений. См. также статью Марии ван Стриен ‘Исчезновение философской проблемы материи в физике конца девятнадцатого века‘:
‘К концу XIX века физики все чаще отвергали вопрос об истинной природе материи, утверждая, что этот вопрос не имеет отношения к физике или вообще не имеет смысла. Иногда это рассматривалось как освобождение физики от философии, а иногда как результат философских размышлений о физике.’
Спектроскопия
При обсуждении связи статистической механики с экспериментами потребуется представление о спектроскопии, то есть, о взаимодействии электромагнитного поля с веществом. Формально спектроскопия восходит к опыту Ньютона по разложению луча солнечного света на составляющие цвета с использованием призмы. В начале 19-го века было обнаружено, что такой спектр содержит линии, как бы разделяющие соседние цвета.
Более систематическое изучение спектральных линий и установление их связи с химическими элементами было проведено Кирхгофом и Бунзеном в 1860-х годах. Рассмотрим конструкцию прибора — это даст необходимое представление о спектрометре (рисунок взят из Вики History of spectroscopy).
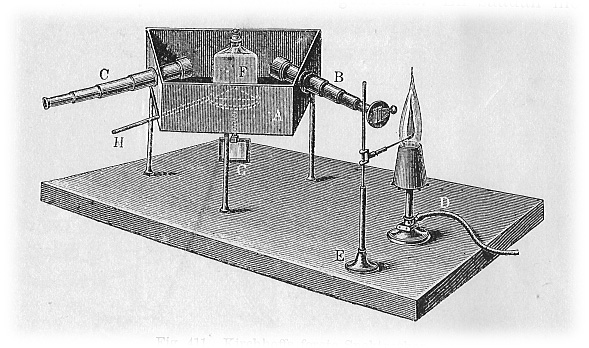
В пламя свечи горелки Бунзена вводится исследуемое вещество с использованием штатива E. Система линз В фокусирует эту часть пламени на призму F, в которой происходит разложение спектра на составляющие. Наблюдение за спектром ведется через увеличительные линзы С. Призма может вращаться с использованием рычага H, при этом зеркальце G позволяет проводить измерение угла вращения.
Прибор Кирхгофа и Бунзена дает представление о идеальном спектрометре — об устройстве, которое пропускает только определенные длины волн и регистрирует их интенсивность. Спектром является график интенсивности от функции длины волн. Для понимания устройства спектрометра требуется знание о взаимодействия электромагнитного поля с веществом, но для дальнейшего будет достаточно понимания о спектроскопии на этом уровне.
При введении вещества в пламя горелки в опытах Кирхгофа и Бунзена появлялся спектр линий, который измерялся при вращении призмы. Было найдено, что появляющийся спектр зависит от введения определенного химического элемента в пламя свечи; спектроскопия в первую очередь стала использоваться для химического анализа. Помимо прочего это открыло возможность к изучению химического состава Солнца и звезд.
Для перехода к квантовой механике важно проведение количественных измерений спектральных линий; наблюдательные физики и математики заметили простые закономерности при описании спектров атомарного водорода с использованием натуральных чисел (серии Бальмера и Ридберга). В 19-м веке отсутствовали объяснения появления спектров, но их существование оказалось одним из мостиков для формирования квантовой механики. Кстати, это еще раз подчеркивает справедливость введения уровня экспериментальной физики.
Фундаментальные постоянные
Макромир и микромир связаны между собой значениями фундаментальных постоянных. Их надежные численные значения появились в первом десятилетии 20-го века и это обстоятельство существенно поменяло отношение физиков к реальности атомов и молекул. Анализ изменений взглядов физиков проведен в книге Смита и Сета ‘Броуновское движение и действительность молекул‘. Книга посвящена анализу экспериментов Перрена по определению числа Авогадро при изучении броуновского движения, но в книге также есть информация общего характера.
В конце 19-го — в самом начале 20-го века статус молекулярно-кинетической теории оставался на уровне полезной гипотезы. Одна из причин была связана с числом Авогадро, которое входило в формализм теории, но в 19-м веке не было экспериментов для определения надежного численного значения этой величины. Были попытки оценки числа Авогадро, но разница между полученными значениями составляла несколько порядков величины.
Ситуация существенно изменилась за первое десятилетие 20-го века. Отличие в численном значении числа Авогадро, определенного разными методами, перед первой Сольвеевской конференцией в 1911 году составляло менее 10%:
- Использование заряда электрона и числа Фарадея;
- Излучение черного тела — теория Планка;
- Эксперименты с альфа-частицами;
- Эксперименты Перрена по броуновскому движению — три разных метода.
Таким образом, после первого Сольвеевского конгресса сомнения в реальности атомов стали признаком альтернативной науки. Бас ван Фраассен в данном случае говорит об эмпирическом обосновании теории — удалось предложить экспериментальное определение всех констант, входящих в теорию. В книге подчеркивается, что именно это обстоятельство сыграло важную роль в принятии атомной гипотезы. В книге есть немало цитат ученых, обсуждающих значимость определения надежных значений фундаментальных постоянных. Я приведу только выразительное высказывание Анри Пуанкаре, сделанное в 1912 году:
‘Многочисленные согласия между результатами, полученными совершенно различными способами, упрочивают наше убеждение [подтверждение атомистических идей]. Еще очень недавно считали себя счастливыми, видя, что найденные числа [Авогадро] имеют одинаковое число цифр; тогда даже не требовали, чтобы первая значащая цифра была та же; сейчас эта первая цифра найдена, и что особенно замечательно, так это то, что пользовались самыми разнообразными свойствами атома.’
Квантовая механика и расчет из первых принципов
Модель атома Бора объяснила спектральные закономерности, найденные Бальмером и Ридбергом. Бор предложил, что электрон в атоме находится только в состояниях с определенной энергией, и что появление спектральной линии вызывается переходом с одного энергетического уровня на другой. Использование значений фундаментальных постоянных, определенных к тому времени (заряд и масса электрона, постоянная Планка), воспроизводило известное значение постоянной Ридберга для атома водорода.
Дальнейшее развитие квантовой механики позволило провести классификацию спектров на электронные, колебательные и вращательные. Это в свою очередь дало связь спектров с суммой по состояниям и в том числе дало объяснение поведению теплоемкостей газов. Таким образом статистическая механика смогла связать спектральные измерения с термодинамическими свойствами газов и тем самым найти связь между совершенно экспериментами, соответствующие разным уровням организации. Спектроскопия дает информацию о молекулярных постоянных, а калориметрия относится к измерениям на уровне сплошных сред. Совпадение термодинамических свойств, рассчитанных на основе молекулярных постоянным с результатами калориметрии для газов явилось огромным успехом развития статистической механики.
Квантовая механика позволяет рассчитать спектры путем решения уравнения Шрёдингера. Появление компьютеров и рост вычислительной мощности положило начало новой исследовательской программе расчета из первых принципов (ab initio). Результаты используются далее в уравнениях статистической механики, что приводит к численным значениям термодинамических и других свойств веществ. В статье 2023 года ‘Расчет из первых принципов свойств газов для прецизионной метрологии‘ говорится, что результаты расчетов свойств гелия из первых принципов по точности превосходят имеющиеся экспериментальные результаты. Правда, при переходе к неону и аргону точность экспериментальных измерений догнать не удается.
Уравнение Шрёдингера и статистическая механика в некоторых случаях позволяет провести расчеты свойств вещества на основе фундаментальных постоянных, что свидетельствует о правильности представления о ядрах и электронах. В то же время возможности расчетов ограничены, поскольку при увеличении числа электронов время расчета и необходимые компьютерные мощности выходят далеко за рамки возможностей. В следующей главе на этом примере проведено обсуждение границы между экстраполяционизмом и радикальным экстраполяционизмом.
Колебательное движение в двухатомных молекулах
В иерархии аппроксимаций статистической механики есть немало наглядных объяснений в духе картины-представления Больцмана. В качестве примера рассмотрим современное объяснение теплоемкостей двухатомных молекул. В главе 2.2 ‘Равновесная статистическая механика‘ говорилось, что в 19-м веке отличие экспериментальных теплоемкостей двухатомных молекул от предсказаний молекулярно-кинетической теории было одним из первых сигналов о неприменимости классической механики для описания движения молекул.
Включение в рассмотрение колебательного движения приводило к завышенным предсказаниям теплоемкости двухатомного газа и экспериментальные теплоемкости при нормальных температурах свидетельствовали в пользу отсутствия колебательного движения. Правда, дальнейшие эксперименты показали, что теплоемкость зависит от температуры. При повышении температуры колебательное движение как бы включалось, а при достаточно охлаждении газа происходило как бы отключение вращательного движения. В этой связи появился термин ‘замороженная степень свободы’. В молекуле существовали степени свободы, которые при снижении температуры переставали быть активными. В классической механике невозможно найти объяснение такому поведению.
Рассмотрим картиночку из Википедии (Спектроскопия в ближней инфракрасной области):

На ней представлена потенциальная энергия в зависимости от расстояния между атомами. Зеленой линией изображено приближение гармонического осциллятора, а синей — реальная кривая, когда увеличение расстояния приводит к диссоциации молекулы. Вид потенциальной кривой получается при решение электронного уравнения Шрёдингера (Раздел ‘Приближение Борна-Оппенгеймера‘ в главе 2.1 ‘Мысленные модели статистической механики‘).
Замораживание колебательной степени свободы объясняется квантованием колебательной энергии. Колебательная энергия может принимать только определенные значения энергии, что подтверждается существованием колебательных спектров. При обычных температурах заселен только нулевой уровень и поэтому колебательная сумма по состояниям ниже граничной температуры остается практически равной единице. При повышении температуры выше граничной начинается заселение более высоких колебательных уровней и появляется вклад колебательной степени свободы в теплоемкость.
Такое объяснение обладает необходимой наглядностью и хорошо соответствует духу картинки-представления Больцмана. Однако на нулевом колебательном уровне расстояние между атомами не фиксировано, поскольку вероятность нахождения двух атомов на определенном расстоянии задается волновой функцией из решения ядерного уравнения Шрёдингера. Таким образом, переход от приведенного объяснения к миру по-прежнему проблематичен — появляется вопрос смысла волновой функции. Более того, такое объяснение возможно только на уровне приближения Борна-Оппенгеймера, при переходе на уровень точного уравнения Шрёдингера пропадает даже такой уровень наглядности.
Ансамбль Гиббса и вероятности
В заключение рассмотрим ансамбль Гиббса — это представление сыграло ключевую роль в появлении связи статистической суммы с термодинамическими свойствами вещества. Начну с описания Гиббса во введении книги ‘Статистическая механика‘, в котором осуществляется переход к ансамблю систем:
‘Можно представить себе большое число систем одинаковой природы, отличающихся друг от друга конфигурациями и скоростями, которыми они обладают в данный момент, и отличающихся не только бесконечно мало, но может быть и так, что охватывается каждая возможная комбинация конфигураций и скоростей. При этом мы можем поставить задачу не так, чтобы следить за отдельной системой во всех последовательно проходимых ею конфигурациях, а чтобы определить, как будет распределено полное число систем по различным возможным конфигурациям и скоростям в любой требуемый момент, если такое распределение было задано для какого-либо момента времени.’
Вопрос связи ансамбля Гиббса и мира остается открытым вплоть до настоящего времени. В особенности это обстоятельство вызывает споры между философами, пытающимися перекинуть мостик от статистической механики к картине мира. Хорошим примером является недавняя статья философов на эту тему с выразительным названием ‘Кто-нибудь может, пожалуйста, рассказать, что сообщает статистическая механика Гиббса?‘.
В учебниках системы, входящие в ансамбль Гиббса, называются мысленными или воображаемыми копиями. Это задает наглядную модель и позволяет далее перейти к рассмотрению использованию формализма на практике. Концептуальная модель ансамбля Гиббса задает частотную интерпретацию распределения плотности вероятности в фазовом пространстве и это также можно сопоставить философии физики Больцмана. Ансамбль Гиббса являются наглядной картинкой-представлением, которая объясняет появление объективных вероятностей (частотная интерпретация) при нахождении связей между микро- и макромиром. Однако, проекция такого представления на реальный мир вызывает серьезные затруднения.
При переходе к миру ансамбль Гиббса должен соответствовать единственной изучаемой системе, поскольку только так осуществляется переход к рассмотрению экспериментов. В результате требуется найти интерпретацию вероятности для единичной системы. Отмечу, что в книге Стивена Браша указывается на роль статистической механики в привыкании физиков к вероятностным представлениям еще до появления квантовой механики.
В статистической механике на качественном уровне рассмотрения существует возможность перехода к частотной интерпретации в случае единственной системе. Момент времени макросостояния связан с интервалом времени, в течение которого проводятся экспериментальные измерения и когда предполагается, что макросостояние не меняется. Такому интервалу времени соответствует огромное количество микросостояний, что вводит определенную статистику для единственной системы.
Конечно, нельзя забывать, что доказать равенство среднего по времени среднему по ансамблю в общем случае в статистической механике не удалось. Также такой подход связан с незнанием человека и, как следствие, приводит к вечному вопрос о статусе вероятности, связана ли она с незнанием человека или вероятность относится к свойству мира. В данном случае можно только указать на успехи статистической механики в рамках объективных вероятностей.
Далее: Глава 4. Горение свечи и уровни организации
Список литературы
Henk W. De Regt, Ludwig Boltzmann’s «Bildtheorie» and Scientific Understanding, Synthese, Vol. 119, No. 1/2, (1999), pp. 113-134.
Людвиг Больцман, Статьи и речи, 1970.
О значении теорий (1890), с. 53-57
Памяти Йозефа Лошмидта (1895), с. 85-105
О неизбежности атомистики в естественных науках (1897), с. 116-131
О статистической механике (1904), с. 163-179
Дюбуа-Реймон, Эмиль Генрих (1818-1896). О пределах познания природы : Лекция, чит. Эмилем Дю-Буа-Реймондом на втором публ. заседании 45 собр. нем. естествоиспытателей и врачей 14 авг. 1872 г. в Лейпциге : Пер. с нем. — Могилев на Днепре : изд. переводчиков, 1873. Загл. ориг.: «Über die Grenzen des Naturerkennes.»
Эмиль Дюбуа-Реймон: Не знаем и не будем знать
Marij van Strien, When Matter Ceased to Matter: The Disappearance of the Philosophical Problem of Matter From Physics in the Late Nineteenth Century. In The History and Philosophy of Materialism, pp. 306-319. Routledge, 2024.
Gabriel Finkelstein: Emil du Bois-Reymond. Neuroscience, Self, and Society in Nineteenth-Century Germany. MIT Press, 2013.
George E. Smith and Raghav Seth, Brownian Motion and Molecular Reality, 2020.
Признание реальности молекул в начале 20-ого века
Bas C. van Fraassen, The perils of Perrin, in the hands of philosophers, Philosophical Studies 143 (2009): 5-24.
Giovanni Garberoglio, Christof Gaiser, Roberto M. Gavioso et al. Ab initio calculation of fluid properties for precision metrology. Journal of Physical and Chemical Reference Data 52, no. 3 (2023).
Roman Frigg and Charlotte Werndl. Can somebody please say what Gibbsian statistical mechanics says? The British Journal for the Philosophy of Science, 2021, 72:1, 105-129.
Steven Brush, The Kind of Motion We Call Heat, 1976.
Обсуждение
